

a placer dans le texte :
un labyrinthe de 4x4 représente un passage par max 16 cellules avec 4 actions par cellule soit au pire un nombre de 16 chiffres. il existe 4 400 10exp9 possibilités.
en 5x5 il y a 1 407 000 10exp9 possibilités.
Le programme d'occupation, lui, oblige de passer par toutes les cellules, donc de trouver 1 nombre parmi des millions de milliards.
Sujets à aborder
ia auto generative
sap learning hub
L'objectif de cette recherche est de comprendre le fonctionnement et les limites de l'intelligence artificielle, ia.
L'intelligence artificielle, ia, est une utilisation informatique de la statistique.
Son premier temps, apprentissage, permet l'analyse de données.
Son second, prédiction, permet l'exploitation des «leçons» du premier.
L'apprentissage est la phase la plus importante.
Elle consiste
à tenter, dans un but précis, un maximum d'actions, sur un maximum d'informations et
d'en mémoriser le meilleur résultat.
Exemple volontairement simple, quoique : la reconnaissance de chiffres manuscrits.
Le but précis = associer un caractère, chiffre, 0 à 9, à une image, écran, photo.
Le max d'informations = le max d'images de chiffres manuscrits.
Le max d'actions = dans ce cas, le max de tentatives, itérations, de classement des images de chiffres.
Le meilleur résultat = la + grande probabilité qu'une image soit prédite dans la bonne classe, par exemple, que l'image d'un 7 soit prédite 7.
Voir le programme C:\Users\Yves\ia\ reconnaissance_chiffres_manuscrits_sklearn.py.
L'apprentissage nécessite l'échantillon le plus volumineux et le plus grand nombre d'itérations possibles.
Il est réalisable aujourd'hui grâce à l'échange de données généralisé et à la puissance immense des ordinateurs.
La prédiction est l'application de l'apprentissage, préférentiellement, à de nouvelles informations.
L'ia rend possible le traitement de données complexes, inimaginable en programmation classique (*).
Voici quelques exemples d'application de l'IA.
Identification : race, variété, espèce, son, image, sécurité, reconnaissance, maladie, symptôme, musique.
Génération : image, animation, son, texte, rédaction, composition, conduite, jeu, guidage, pilotage, traduction.
(*) La différence, entre programmation classique et apprentissage, est que la classique est déterministe, si, et, ou, alors, sinon, tant que, jusque, alors que l'apprentissage est
statistique.
La différence essentielle est que pour beaucoup de cas, la programmation traditionnelle nécessite des millions de lignes de code et l'apprentissage
un nombre extrèmement réduit.
Par exemple, j'imagine difficilement programmer la reconnaissance d'un chiffre manuscrit. Par contre j'ai vu un programme d'apprentissage de 86 lignes de code
capable de classer les images par chiffre.
Suite à l'apprentissage, le programme de prédiction va, pour une image d'un 7, choisir la classe des 7, avec un taux de confiance de 94%.
Voici des exemples d'apprentissage, du plus simple au plus compliqué.
Avant
Après
C'est le cas le plus simple et le plus compatible avec l'imagination.
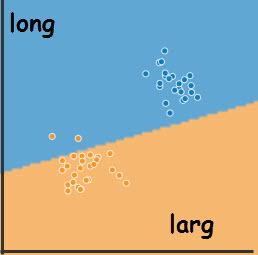
Supposons qu'il faut détecter sur une route, limitée à 3,5t, les véhicules en infraction et les signaler à une patrouille de police.
Une caméra à l'entrée est capable de mesurer la longueur et la largeur de chaque véhicule.
Cette caméra transmet, au fur et à mesure, les dimensions à un programme de prédiction.
Comment faire en sorte que ce programme avertisse à bon escient ?
En IA, il suffit de rassembler dans un fichier, matrice, un max de dimensions de véhicules, en indiquant, supervision, si ils dépassent 3,5 t.
On utilise cette matrice dans un programme d'apprentissage qui partage les dimendions en 2 classes, binaire, séparées par une droite, linéaire.
Dans les illustrations, les largeurs sont en abscisses et longueurs en ordonnées.
Avant exécution, les points bleus, >3,5t, et oranges, <3,5t, sont visiblement séparés. Cependant, la frontière entre les 2 classes est initialisée au hasard et des points
oranges sont en zone bleue.
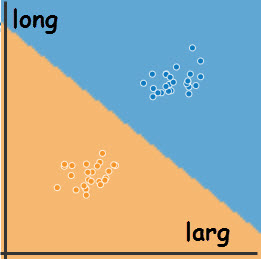
Après les savants calculs, les deux classes sont correctement séparées par une frontière de décision linéaire, représentant l'équiprobabilité d'appartenance à une classe.
Ces informations sont utilisées par le prédicteur qui avertit la patrouille chaque fois qu'un véhicule de la zone bleue, probablement > 3,5t, est caméräisé.
Un esprit chagrin pourrait remarquer que les dimensions ont changé «en cours de route». C'est vrai car les points d'avant et ceux d'après sont extraits de deux tests.
J'avoue que j'ai la flemme de recommencer les copies d'écran.
Cependant, à quelque chose malheur est bon. Ça accentue l'importance de l'échantillon d'apprentissage. Il doit être le plus complet possible pour minimiser le risque d'erreur.
Dans la famille des binaires, biclasses, il y a aussi des frontières de décision inlinéaires.
En voici deux exemples, avec la situation avant, la situation après apprentissage linéaire et la situation après apprentissage complexe.
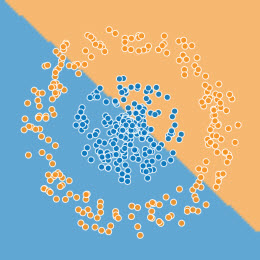
État initial
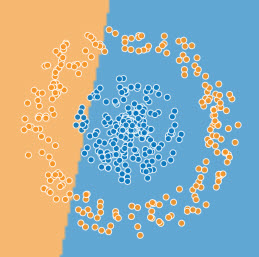
À l'abandon d'une tentative linéaire infructueuse

Après apprentissage inlinéaire
Exemple 1 d'apprentissage binaire, inlinéaire
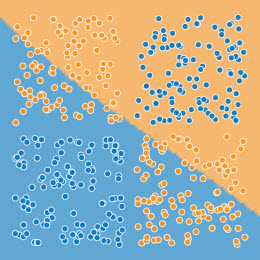
État initial

À l'abandon d'une tentative linéaire infructueuse

Après apprentissage inlinéaire
Exemple 2 d'apprentissage binaire, inlinéaire
La différence de résultat saute aux yeux.
Il est inimaginable d'utiliser une prédiction issue d'un apprentissage linéaire dans ces cas.
Je ne veux pas mettre systématiquement en doute l'IA mais je me demande si elle est capable de changer de méthode en cas d'échec. Dans ces exemples, un humain voit que la linéarité est inadaptée et ne perd pas son temps.
Ce qui précède sert à imaginer l'apprentissage grâce à des exemples en 2 dimensions.
L'esprit humain peut imaginer deux dimensions, le plan. Il peut imaginer 3 dimensions, le volume, longueur, largeur, hauteur. Il peine avec 4 dimensions, un volume au fil du
temps. Mais à partir de 5 c'est le trou noir.
Que dire d'un échantillon d'images de 64x64, 4 096 dimensions ?
Théoriquement, le nombre de dimensions est illimité.
Les 3 exemples précédants font partie de la famille «de classification». Cette famille calcule les frontières des classes afin que tout point, quelque soit le nombre de dimensions, appartienne à une classe. C'est cette classe qui sera prédite le moment venu. C'est cette famille d'apprentissage qui permettra de prédire, avec une certitude de 94%, que cette image, de 64 dimensions, est celle d'un chiffre 7 manuscrit. La classification est très répandue en ia mais n'est pa la seule.
Il existe 3 modes d'apprentissage, supervisé, insupervisé et par renforcement.
Je commence par le plus facile à comprendre.

Avant

Après
Apprentissage supervisé d'une classification binaire linéaire
Dans le but de frapper les esprits, un module, programme élémentaire, de ce type est appelé neurone artificiel. C'est surtout artificiel mais je conserve l'appellation, utile pour la suite.
Pour comprendre le principe, ou s'en souvenir, voir
https://www.youtube.com/watch?v=VlMm4VZ6lk4&t=0s.
En résumé :
L'échantillon fournit des constantes, les points, coordonnées x1x2, qui forment 2 «nuages».
En apprentissage supervisé, chaque point a une couleur, étiquette, orange, bleue.
Le but de l'apprentissage binaire linéaire, est de tracer une frontière droite permettant de prédire, vu ses x1x2, si un point est orange, ou bleu, avec la meilleure
probalilité.
Sachant que tous les points d'un côté sont censés appartenir à la classe 0, orange, et de l'autre à la classe 1, bleue, un humain ordinaire, comme moi, comprend que la
frontière doit être aussi éloignée que possible de chacun des points et qu'il faut maximiser la somme des écarts.
Compte tenu des capacités de l'informatique, les penseurs ont opté pour l'inverse, la minimisation du risque d'erreur.
Le risque d'erreur est la probabilité que toutes les prédictions soient fausses, tous les oranges en bleue, tous les bleus en orange.
Pour faire encore plus simple, ils ont choisi d'additionner des logarithmes plutôt que de multiplier des probabilités et ont inventé le log loss, LL.
La meilleure frontière est donc celle qui a le plus petit LL .
La formule choisie pour la frontière de décision est w1X1 + w2X2 + b = 0.
X1 et X2 étant des constantes, la programmation permet d'analyser l'influence des variables, coefficients, poids, wi, et du biais, b, sur l'évolution du LL.
Elle permet d'augmenter la variable si son augmentation favorise une diminution du LL, sinon elle doit la diminuer.
Ce calcul s'appelle le gradient.
À l'issue de ce calcul, chaque coefficient, et le biais, sont légèrement modifiés, descente de gradient, en fonction d'un taux d'apprentissage,
learning rate.
Ces modifications provoquent le changement de droite qui donne lieu à de nouveaux calculs, boucle d'apprentissage.
Cette boucle est interrompue, idéalement, lorsque LL est tombé à 0. Lorsque l'apprentissage est imparfait, le LL cesse de diminuer, voire augmente.
Je récapitule les étapes de la boucle d'apprentissage :
1) Agrégation de toutes les variables selon la formule z = w1x1 + w2x2 + b.
2) Activation, calcul de probabilité de z et prédiction de 1 si z >= 0,5.
3) Calcul du risque sur tout l'échantillon d'apprentissage, LL.
4) Calcul des gradients. Estimation de la variation du LL en fonction de la modification du poids wi, et du biais, b, b est l'ordonnée de la droite lorsque X1X2 = 0.
5) Calcul et mise à jour des wi et b.
6) Agrégation suivante.
Ce sont les wi et b, après apprentissage, qui déterminent la droite de décision, w1x + w2y + b = 0, frontière d'équiprobabilité, entre les 2 zones.
Apprentissage supervisé d'une classification binaire inlinéaire
Dès que la frontière de décision n'est plus une doite, le neurone ne suffit plus. Il faut en utiliser plusieurs et former un réseau.
Voici un exemple simple, mais spectaculaire.

Lorsque une droite ne suffit plus, points oranges en zone bleue,
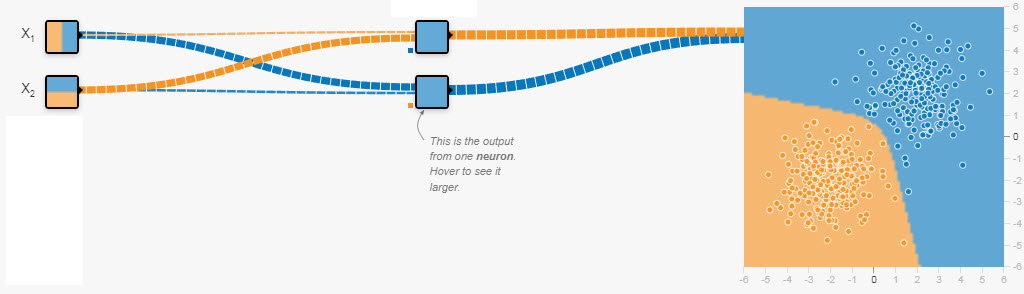
il suffit d'ajouter des couches et des neurones.
La première image représente un neurone, à droite, recevant directement les valeurs X1 et X2. Il les traite de façon binaire et linéaire, avec le résultat insuffisant,
des points oranges restent en zone bleue.
La seconde image illustre un réseau. Les valeurs X1 et X2 sont traîtées par 2 neurones de la 1ère couche qui envoient leurs prédictions au neurone final, avec un résultat
impressionnant.
Dans un réseau, tous les neurones fonctionnent de la même manière, décrite précédemment.
La nouveauté est
- que le neurone envoie sa prédiction à tous les neurones suivants, propagation avant, et
- que le LL, les gradients et les màj de wi, et b, sont étendus à tout le réseau, propagation arrière.
Le nombre de couches et de neurones est illimité.
Ce fonctionnement en réseau est conceptuellement, mathématiquement et informatiquement très simple avec des résultats qui me laissent pantois.
Le second schéma mérite les précisions suivantes :
1) à gauche se trouvent les valeurs de l'échantillon, de 1 à n, illimité, 64 pour une image de 8x8, 2 ici;
2) au centre se trouvent les couches internes du réseau, dites cachées, ici 1 couche de 2 neurones, illimités dans la pratique;
3) à droite se trouve le résultat de la classification, zones colorées, ici 2, illimité dans la pratique;
4) les lignes symbolisent la transmission des données, leur poid, positif ou négatif;
5) la carré au bas, inférieur gauche, des neurones représente le biais, plus ou moins positif ou négatif.
Pour observer et chercher à comprendre, en 2D, voir
http://playground.tensorflow.org/.
Après cette premiere approche, je me dis que l'IA supervisée permet de la classification, multidimensionnelle, à fin de prédiction
L'apprentissage insupervisé. À voir https://www.youtube.com/watch?v=FTtzd31IAOw.

Le poids, X1, le nombre de pattes, X2,
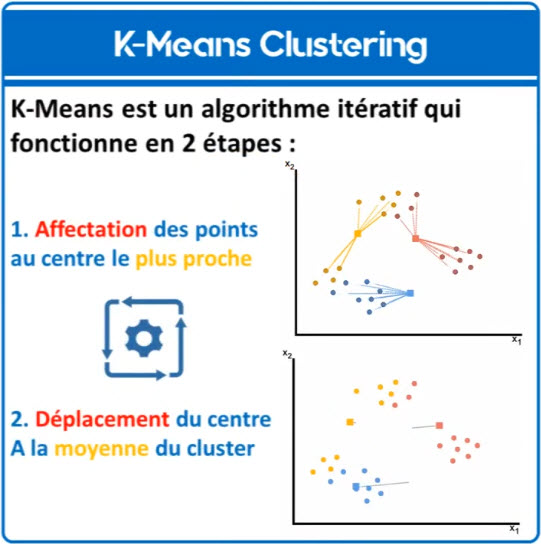
sans préciser de quoi il s'agit
pourtant, le programme distingue 3 groupes et leur limite
Le regroupement
Il s'agit de regrouper des données en fonction de leur ressemblance, création d'ensembles d'éléments ayant des points communs.
Cela peut servir à suggérer des groupes afin qu'un utilisateur y colle des étiquettes, après avoir examiné les caractéristiques ?
Les résultats peuvent alors servir à de la classification supervisée.
Autre idée, la proposition d'achat, de lecture, de contenu, «Ceci pourrait aussi vous intéresser», ou autre suggestion du même acabit.»

Une méthode de détection,

tracer une limite, au hasard.
La détection d'anomalie
Pour détecter les taches dans le décor, ce qui n'a rien à faire dans l'échantillon d'apprentissage.
Son usage me paraît plus évident. Sécurité, individu armé dans un endroit public, voiture dans un piétonnier, aiguillage des déchets.
.
La réduction de dimension
Réduire le nombre de variables réduit les volumes des traitements supervisés.
La réduction s'appuie uniquement sur les caractéristiques sans avoir besoin du quoi il s'agit.
Le but de cet apprentissage est de permettre à un programme de prédiction, d'établir la meilleure action à accomplir dans un état donné.
Ce programme prédit grâce à une matrice, table, de décision.
Par exemple :
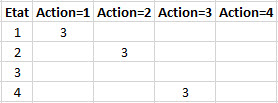
La matrice fixe la règle à suivre.
D'après cette matrice, c'est l'action = 1 qui à la meilleure note en état 1, l'action = 2 en état 2, l'action = 3 en état 4, ....
Il prédira, donc, 1 en état 1, 2 en état 2, rien, pas de panique, en état 3 et 3 en état 4.
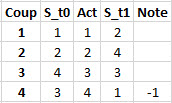
L'historique des états.
La mise à jour de la matrice est déclenchée lorsqu'une note, facultative, est attribuée.
Cette note renforce, ou déforce, selon une logique programmée, tous les états rencontrés, en remontant jusqu'à l'état initial.
Dans cet exemple simple, une note négative, -1, est attribuée lorsque l'action provoque un dépassement de limite ou un retour à un état déjà rencontré.
La logique programmée est d'attribuer aux états initiaux précédants le nombre de coups innotés, ici 3.
Cela donne la matrice du début.
Si un essai est l'application d'une action dans une situation initiale,
il faut comprendre que cette logique de renforcement est basée sur un très grand nombre d'essais, au moins autant que nécessaire pour éprouver toutes les actions
dans toutes les situations initiales.
Dans cet exemple simple, les actions sont toutes générées aléatoirement.
Par exemple :
3,1,2,2,3,4,2,1,4,2
donnant comme trace :
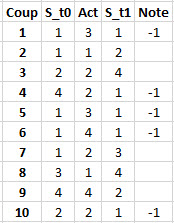
L'historique des états.
Nous avons 5 notes, donc 5 passages par la logique de màj, mais aucun renforcement, une màj antérieure ayant déjà enregistré une suite de 3 coups innotés, moins est insuffisant.
Le programmeur estime que la première suffit, donc stop.
Mais que se passe-t il dans cet exemple ?
Pour bien comprendre, un petit dessin vaut mieux ...
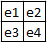
Le terrain de jeu.
Dans cet exemple, didactique, 4 actions sont possibles, →, 1, ↓, 2, ←, 3, ↑, 4. Tout est il clair, à présent ?
Le programmeur doit concevoir un apprentisseur qui, au départ de l'e1, avec les 4 actions possibles, 1, →, 2, ↓, 3, ←, 4, ↑, passe par tous les états, sélectionne toutes
les cases, du tableau de jeu, quelles qu'en soient les formes et dimension.
En v1, le déplacement est entièrement aléatoire avec retour au début à chaque erreur.
Dans ces conditions, l'apprentissage est interminable, à partir de 5x5.
En v2, le déplacement est dans l'ordre numérique croissant parmi les actions possibles. L'apprentissage ne dure plus que quelques secondes, même pour les tableaux les
plus grands.
Cette énorme différence illustre l'importance du choix de l'algorithme par le programmeur.
Voir les programmes suivants : C:\Users\Yves\ia\occupation_apprentissage_v1.py, C:\Users\Yves\ia\occupation_demo.py et C:\Users\Yves\ia\occupation_apprentissage_v2.py.
Le programmeur doit concevoir un apprentisseur qui, au départ de la position initiale, avec les 4 actions possibles, 1, →, 2, ↓, 3, ←, 4, ↑, parvient à sortir d'un labyrinthe.
Je suis parti, au départ, du principe du programme d'occupation et puis j'ai pensé que dans un labyrinthe, l'apprenti sait où sont les murs infranchissables et connaît donc les
directions possibles.
J'ai donc imaginé une matrice lignesxcolonnes ou chaque cellule contient un vecteur indiquant les actions possibles.
Par exemple, dans un couloir horizontal, droite, gauche.
Dans un couloir vertical, bas, haut. Dans un carrefour, droite, bas, haut. ... .
Principe acceptable intellectuellement mais pas facile à réaliser.
Pour y arriver, j'ai adapté un programme de création de labyrinthe existant, merci au généreux auteur.
Il y a 4 programmes.
1- Création v2, qui crée la matrice et les vecteurs pour l'apprentissage et la démo.
2- Apprentissage v1, qui choisit les actions dans un ordre croissant constant.
3- Apprentissage v2, qui tire les actions au sort.
4- Démo, qui utilise le vecteur d'expérience issu de l'apprentissage.
Il n'y a pas de différence systématique entre les 2 apprentissages.
Si, à priori, la v1 favorise la descente de gauche à droite et défavorise le sens inverse, la v2 qui part au hasard, ne prend jamais franchement l'avantage.
Les résultats sont comparables et, surtout, fonction du labyrinthe.
Ce jeu est une belle démonstration de l'ia.
Pas d'intelligence mais une capacité d'essayer des millions de possibilités, pendant que l'humain écarquille les yeux, en se demandant comment s'y prendre.
Voir les programmes suivants :
C:\Users\Yves\ia\labyrinthe_creation_v2.py,
C:\Users\Yves\ia\labyrinthe_apprentissage_v1.py.
C:\Users\Yves\ia\labyrinthe_apprentissage_v2.py.
C:\Users\Yves\ia\labyrinthe_demo.py.
Les 2 joueurs, prennnent, à tour de rôle, entre 1 et 3 allumettes.
Celui qui prend la dernière perd la partie.
Dans le jeu des allumettes, l'état de l'apprenti en t+1 dépend de l'action
de l'apprenti ET de celle son adversaire.
Je pressens que plus l'adversaire est coriace et plus l'apprentissage
est efficace.
Je programme donc, à fin de comparaison, 3 apprentissages.
1) aap mode aléatoire pur : apprenti aléatoire contre adversaire aléatoire.
2) aal mode aléatoire limité : apprenti aléatoire contre
un adversaire aléatoire mais pas suicidaire. En 3 il prendra 1 ou 2,
au hasard. En 2, il prendra toujours 1.
3) exp apprenti aléatoire contre l'expert : aucune erreur n'est permise.
Dès qu'il peut, il met l'apprenti dans une position fatale, en 9 ou 5
ou 1.
S'il est lui-même en position fatale, il agit aléatoirement, sauf en 1,
où il joue 1.
J'ai testé le pur aléatoire et ai constaté que l'apprenti n'apprend rien. Il
peut commettre les pires erreurs et gagner malgré tout. Par exemple, je
ne comprenais pas, être en 4, prendre 1 et gagner. En y réfléchissant, le
pauvre adversaire avait perdu parce que le hasard lui a fait prendre 3.
Chaque apprentissage crée une matrice d'expérience qui peut, ensuite,
être testée.
Je teste les 5 combinaisons dignes d'intérêt.
Méthode d'apprentissage
----------------------------
/!\ TRES IMPORTANT La machine ignore ce qu'il se passe.
À son tour de jouer, elle dispose de son état initial, nombre,
et doit accomplir une action, nombre.
L'environnement lui retourne son nouvel état et un bonus/malus éventuel.
Son programme d'enrichissement doit valoriser, ou dévaloriser, les actions,
et états, antérieures pour qu'en exploitation, lorsqu'elle sera dans l'état
initial elle accomplisse l'action la plus avantageuse.
Dans ce jeu, l'apprenti apprend toujours par des actions aléatoires et je
compte simplement le nombre de victoires, par action, au départ de l'état.
Objectif de l'exécution
---------------------------
aap apprentissage aléatoire pur, apprenti, et adversaire, aléatoire.
aal apprentissage aléatoire limité, adversaire insuicidaire.
exp apprentissage expert, adversaire expert.
taap1 test aap contre aléatoire limité
taap2 test aap contre expert
taal1 test aal contre aléatoire limité
taal2 test aal contre expert
texp1 test exp contre expert
Observations
---------------
Sur 2000 parties, les victoires, en apprentissage puis en test, en moyenne,
| taap1 | 1000 | 1400 |
| taap2 | 1000 | 0 |
| taal1 | 550 | 1900 |
| taal2 | 550 | 0 |
| texp1 | 75 | 2000 |
Haut