

Mode d'emploi
Les soulignementsLes soulignements
peuvent indiquer un lien explicatif.
peuvent indiquer un lien explicatif.
CliquerCliquer peut être instructif.
peut être instructif.

IPV ?
L'objectif de cette recherche est de comprendre la situation des installations photovoltaïques wallonnes.
Où se trouve la vérité entre les chants de sirène du ministre de l'énergie de Wallonie, André Antoine, en 2007
(https://www.youtube.com/watch?v=dVTLfYjuvb4) et les cris d'orfraie du président du parlement de Wallonie,
André Antoine, le même, en 2016 ?
Pour interrompre prématurément les aides accordées aux producteurs et, pire que ça, pour les faire cracher au bassinet, leurs détracteurs, politiciens, ministres et
gestionnaires de réseaux, utilisent deux arguments que je souhaite vérifier.
-1- Il paraîtrait que les installations photovoltaïques, IPV, sont un péril technique pour les réseaux qu'il va falloir renforcer, en dépensant des fortunes.
-2- Il paraîtrait, par ailleurs, que le financement des certificats verts, CV, constitue un gouffre financier injustement supporté par les malheureux qui ne produisent pas
d'électricité photovoltaïque.
Imaginer sans cesse les migrations de forces, d'électrons et leurs effets .
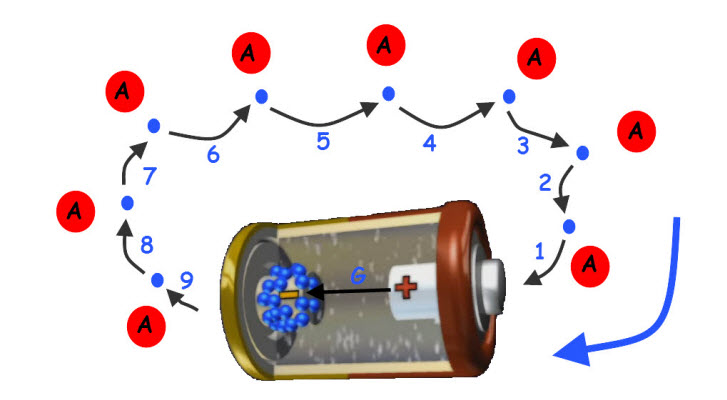
Circuit d'électrons avec huit atomes A
L'électron 1 rentre dans la pile, 2 remplace 1, ..., 8 remplace 7 et 9 sort de la pile
(électricité, courant, circuit, générateur, récepteur, conducteur, effet, échauffement, champ magnétique, intensité, ampère, coulomb)
L'électricité est une double migration, d'électrons et de forces électromotrices, déclenchée par un générateur.
(Animation d'Hydro Québec Comprendre l'électricité, à partir de 21 secondes).
Un générateur de tension crée une forces électromotrice, fem, initiale qui déplace le premier électron. Par une réaction en chaîne, chaque électron, en quittant
sa place, crée un trou, une fem, qui attire l'électron suivant.
La suite est une répétition d'électron déplacé ⇒ fem.
Ce n'est pas la force du générateur qui déplace le dernier électron mais la force induite par son prédécesseur.
Les alternateurs décrits par la suite sont des générateurs de tension. Il existe aussi des générateurs de courant. Le générateur de courant déplace les premiers
électrons qui induisent de la fem et une réaction en chaîne. Les cellules PV seraient plutôt dans cette catégorie car ce sont des photons qui déplacent les
premiers électrons. Cette nuance n'a pas d'importance dans le cadre de cette recherche.
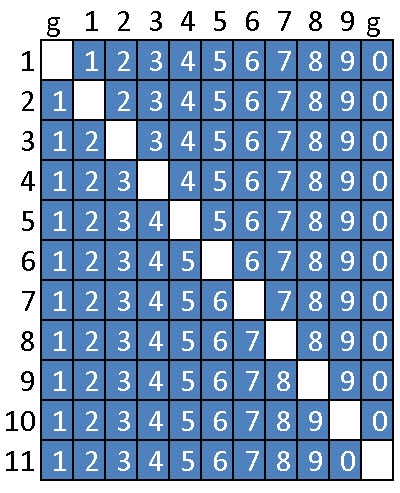
Double migration en onze étapes
L'électron le plus proche happé par
le trou en crée un nouveau
La migration d'électrons constitue le courant électrique. Chaque électron, en se déplaçant, forme une minuscule partie de ce courant, un micro-courant, μcourant.
La fem du générateur crée le premier μcourant. La suite est une répétition de μcourant ⇒ fem.
femg ⇒
μcourant1 ⇒ fem1 ⇒
μcourant2 ⇒ fem2 ⇒
... ⇒
μcourantn ⇒ femn ⇒ ...
Garder à l'esprit que μcourantn n'est pas μcourant1 mais sa descendance. Ils sont parents mais différents.
femn n'est pas femg mais sa descendance. Elles sont parentes mais différentes.
Ces nuances seront très utiles plus tard.
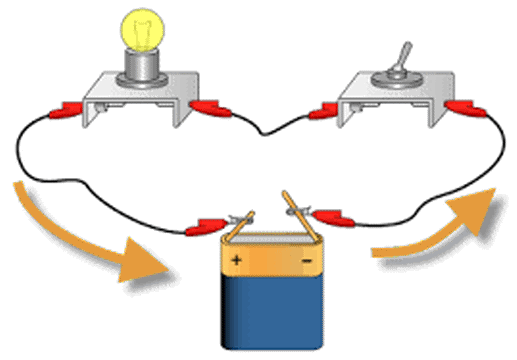
Circuit constitué d'un générateur -une pile-,
un conducteur -trois fils et un interrupteur-
et un récepteur -une ampoule-
De la lampe de poche aux réseaux internationaux, du plus simple au plus complexe, l'électricité nécessite un circuit fermé comprenant, au minimum, un générateur,
comme une pile, un récepteurLe récepteur utilise l'électricité contrairement au conducteur qui ne fait qu'assurer son passage.,
comme une ampoule, et les conducteurs, les fils, pour les relier.
Même s'il est le plus souvent très classique, un circuit peut aussi prendre les formes les plus inattendues. L'électricité peut, par exemple, passer par le sol (prise de terre) ou par le corps (électrocution) ou à travers l'air (éclair). S'il y a de l'électricité, c'est qu'il y a un circuit fermé, même au travers de matériaux qualifiés d'isolants.
L'électricité a deux effets principaux : échauffement et champ magnétique.
Lorsqu'ils se déplacent, les électrons se frottent partout, se cognent à tout et produisent l'échauffement des endroits où ils passent. Plus ils sont nombreux
à se déplacer et plus ça chauffe. Cet échauffement s'appelle l'effet de Joule.
La fem induit un champ magnétique. Ce champ est amplifié lorsqu'elle se déplace dans un bobinage. Cette propriété est utilisée par les
moteurs, les transformateurs et les électro-aimants.
Tout courant électrique, alternatif ou continu, génère un champ magnétique (Courants électriques et magnétisme).
Le débit du courant, le nombre d'électrons par seconde, passant à un endroit, détermine l'effet du courant à cet endroit. Plus le débit est grand
et plus l'effet est important.
Le débit du courant, son intensité, est exprimé en ampères. Un ampère (A) représente le passage d'un coulomb (C)1 C = 6,24x1018 e-. Plus de six milliards de milliards d'électrons.
par seconde (s)(1A = 1C / 1s).
Pour limiter l'échauffement, l'intensité maximale d'un raccordement ordinaire, la maison de Monsieur Dubois, est limitée à 40 A. Au delà, un fusible fond, ou un disjoncteur
disjoncte, et ouvre le circuit, ce qui coupe le courant.
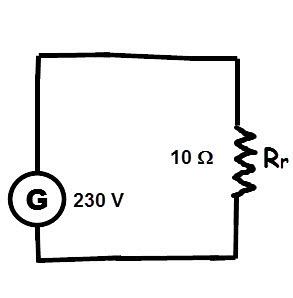
I = E /R = 230 / 10 = 23 A
(force électromotrice, fem, volt, résistance, ohm, loi d'Ohm, résistivité, montage en série, tension, différence de potentiel, ddp)
Pour entretenir la double migration, il faut une force électromotrice, fem, E qui est mesurée en volts (V).
L'intensité (I) du courant est proportionnelle à la force électromotrice (E (V)). Le facteur de proportionnalité s'appelle la résistance (R) et est mesuré en
ohms (Ω). Cette loi de l'électricité s'appelle loi d'Ohm et s'énonce E (V) / R (Ω) = I (A).
La résistance d'un conducteur peut être calculée à l'aide de la formule R = ρ (Ω.m) x L (m) / S (m2). La
résistivité
Les conducteurs ont une très faible résistivité (17.10-9 Ω.m pour le cuivre). Les isolants ont une très forte résistivité (1010 Ω.m
pour le caoutchouc).
ρ
est fonction du matériau (Ω.m). L est la longueur (m) et S la section (m2).
1 volt est la fem capable d'induire un courant d'1 A dans une résistance d'1 Ω.
Il s'agit, en ce début de recherche, de la loi d'Ohm originelle. Elle est applicable dans la majorité des cas.
Tous les cas possibles sont couverts par la loi d'Ohm généralisée, où l'impédance remplace la résistance. Ces notions sont abordées plus loin.
R = ΣRn
E = ΣVn
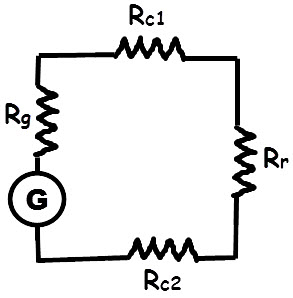
Ce modèle plus complet de circuit montre que la résistance est composée d'une série de résistances cumulées. Il y a celle, interne, du générateur, celle du premier conducteur,
celle du récepteur et celle du second conducteur.
Comme il n'y a qu'un seul chemin, la force doit affronter successivement chacune des difficultés. Chaque épreuve épuise la force qui diminue progressivement.
Cette configuration de circuit est appelée montage en série.
Exemple : une lampe à incandescence au bout d'un câble de 20 m. Rg pour le générateur, Rc1 pour le fil 1, Rr pour la lampe, Rc2 pour le fil 2.
La résistance totale,eq pour équivalente, Req (Ω), équivaut à la somme des résistances des composants : Req = Σ Rn = Rg +
Rc1 + Rr + Rc2.
Le courant, I (A), est unique et déterminé par la loi d'Ohm : I (A) = E (V) / Req (Ω)
= Ig = Icn = Ir.
La fem peut être désignée de trois façons. Elle est mesurée en V dans les trois cas.
La fem est produite au coeur du générateur et représentée par la lettre E.
Entamée par la traversée du générateur, voire par le long chemin parcouru pour parvenir à destination, elle est appelée tension
et représentée par la lettre U. D'habitude, tension désigne une mesure à une borne de générateur, une prise de courant ou tout autre endroit conçu pour fournir
du courant, transformateur du réseau, compteur électrique, prise.
Partout ailleurs, sa diminution, entre deux points quelconques, est appelée différence de potentiel, ddp, et représentée par la lettre V.
Formules
La résistance équivalente, totale, est composée de la résistance interne du générateur et du reste, la résistance externe.
Req = Rg + (Rc1 + Rr + Rc2) = Rg + Rext.
E = Σ Vn
E - Vg = U = Vext = Rext x I
Mesure de E et calul de Rg
E peut être mesurée en circuit ouvert, I = 0 et E = U.
En mesurant Rext, Rext = Rc1 + Rr + Rc2, et U, I = U / Rext et Rg = (E - U) / I.
Exemple de calcul de Rg
Supposons que E = 12 V, U = 10 V avec Rext = 10 Ω.
1) I = 10 / 10 = 1 A.
2) Rg = (12 - 10) / 1 = 2 Ω
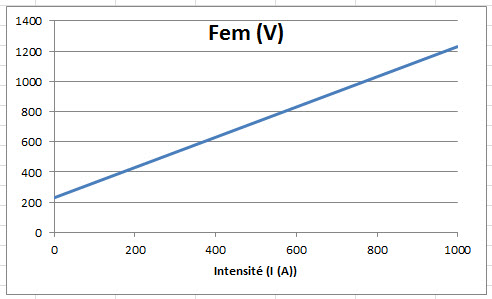
Pour assurer 230 V, il faut faire varier la fem en fonction de la charge
Lorsque la charge augmente la tension diminue, selon une droite, U = E - (Rg x I).
En U.E., Union Européenne, la tension garantie, à chaque raccordement, est 230 V ± 10 %, entre 207 et 253 V. Qui dit tension constante dit fem variable.
Plus la charge augmente et plus la fem augmente, E = U + (Rg x I).
La fem n'est pas une constante. L'intensité n'est pas limitée par la fem mais, au contraire, l'intensité détermine la fem.
Cette contrainte constitue la première constatation très surpenante de cette recherche.
La conception du réseau électrique pour satisfaire cette contrainte est décrite par la suite.
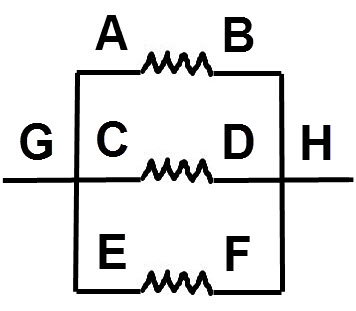
La ddp est la même pour chaque résistance
Le courant total égale la somme des courants
(montage en parallèle)
Pour faciliter la fabrication des appareils, des équipements, des installations, la tension domestique a été normalisée, 230 V en U.E..
Pour que tous les récepteurs reçoivent leurs 230 V standard, ils doivent être tous branchés en parallèle.
Exemple : une prise multiple avec trois lampes à incandescence. RAB pour la lampe 1, RCD pour la lampe 2, REF pour la lampe 3.
Dans un montage en parallèle :
la différence de potentiel, VGH (V), est identique pour chaque résistance : VGH = VAB = VCD = VEF ;
le courant total, IGH (A), égale la somme des courants des composants : IGH = Σ In = IAB + ICD + IEF.
Trois chemins donc trois courants. Tout ce qui entre en G est réparti puis regroupé puis sort en H.
Le corollaire de ces deux règles est la formule précieuse de la résistance équivalente.
Req = 1 / Σ (1 / Rn).
Supposons que la ddp des lampes soit VGH = 10 V avec RAB = 2 Ω, RCD = 3 Ω, REF = 5 Ω.
Le courant de chaque résistance, In (A), est déterminé par la loi d'Ohm : In (A) = VGH (V) / Rn (Ω).
1) IAB = VGH (V) / RAB (Ω) = 10 / 2 = 5 A. ICD = 3,333 A. IEF = 2 A
2) IGH = Σ In = 10,333 A.
3) Req = 1 / Σ (1 / Rn) = 10 / 10,333, cqfd.
Deux lampes de R = 10 Ω et conçues pour une batterie de 12 V.
Avec une seule lampe, I = 12 / 10 = 1,2 A.
Avec deux lampes en parallèle, I = 2,4 A.
En parallèle, la résistance équivalente diminue et l'intensité augmente !
La multiplication des récepteurs et des raccordements en parallèle entraîne, en tendant la résistance équivalente vers 0 Ω, une augmentation potentiellement illimitée de l'intensité.
Tous les appareils domestiques, en U.E., sont alimentés par une tension constante de 230 V ± 10 %.
Pour que ce soit possible, ils sont raccordés en parallèle.
Dans ce cas, I = Σ In, Req = 1 / Σ (1 / Rn) et U = Req x I = Rn x In.
Le transport de la fem au travers du circuit est un raccordement en série.
Dans ce cas, E = U + (Rg x I) et le générateur adapte la fem aux besoins.
Pour avoir un ordre de grandeur, imaginer 200 maisons avec U = Un = 230 V, Rg = 1 Ω, 0 A ≤ In ≤ 40 A.
I = Σ In donc 0 A ≤ I ≤ 8000 A et 230 V ≤ E ≤ 8230 V.
Il existe trois façons de produire de l'électricité. La chimique, la mécanique et la photovoltaïque.

La première pile de l'histoire
La chimique est arrivée la première. Des piles de réactifs divers entassent des électrons d'un côté, électrode ou pôle négatif, en les prélevant de l'autre,
électrode ou pôle positif. A la fermeture du circuit, l'électrode en souffrance attire les électrons les plus proches, déclanche la réaction en chaîne qui aboutit
au prélèvement d'électrons à l'électrode où ils sont en surplus.
Le courant obtenu est constant, continu, aussi longtemps que dure la réaction chimique. Petit à petit la réaction ralentit, l'entassement d'électrons, la fem, diminue et
le courant faiblit.
Les piles actuelles descendent de cette découverte.
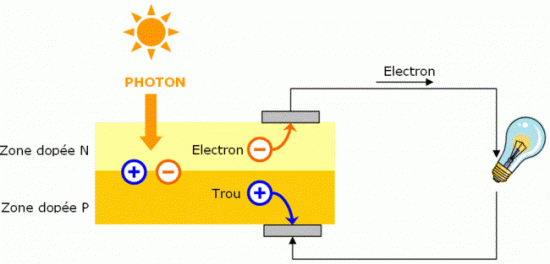
Schéma de l'effet photovoltaique
La photovoltaïque est la plus récente. La cellule photovoltaïque est composée de trois couches. La couche N qui capte les électrons. La couche P qui accumule les trous.
La jonction N-P. Lorsqu'un photon cogne la cellule à un endroit de la jonction N-P, il éjecte un électron, -, de son trou, +. L'électron part dans la couche N et le trou dans
la couche P. Comme dans une pile, il naît une fem entre les couches N et P.
Le courant obtenu est constant, continu, pour un éclairement donné. Quand l'éclairement diminue, l'entassement d'électrons et de trous, la fem, diminue et le courant faiblit.
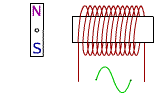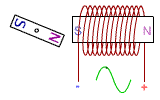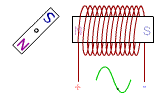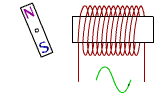
Production de courant par un aimant
en rotation auprès d'une bobine
Ce qui suit vaut pour le courant alternatif mais aussi pour le courant continu. Le continu "mécanique" n'est en fait qu'une somme d'alternatifs. L'explication se trouve à la fin du paragraphe.
La rotation d'un aimant près d'une bobine peut être décomposée en phases répétitives de quatre temps :
1- l'approche du pôle nord,
2- l'éloignement du pôle nord,
3- l'approche du pôle sud,
4- l'éloignement du pôle sud.
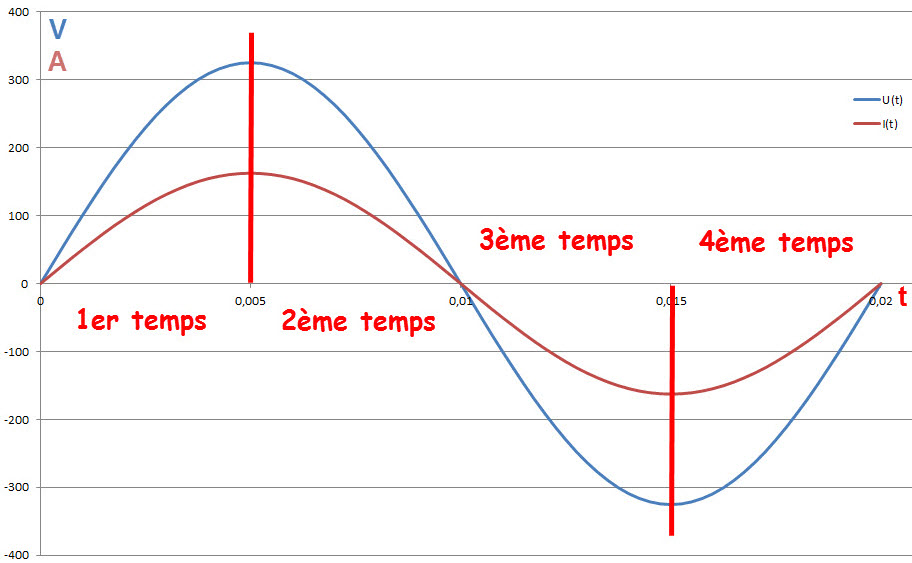
Une phase de quatre temps du courant alternatif, sans déphasage, φ = 0
1- l'approche du pôle nord
La force électromotrice d'attraction des électrons augmente progressivement. Des électrons s'approchent, de plus en plus nombreux et entrent dans la bobine.
Il se produit alors une réaction en chaîne. L'électron qui quitte son atome libère une place et crée un atome qui a besoin d'électron, et exerce une fem. Cette fem attire
à son tour un électron proche. De proche en proche, des milliards de fem et d'électrons se déplacent, au travers du circuit, jusqu'à ce que les atomes "en manque" récupèrent
des électrons à la sortie de la bobine.
Dans ce premier temps, la fem et l'intensité augmentent.
La réaction en chaîne se propage à la vitesse de la lumière, 300.000 km par seconde. A l'échelle belge, le mouvement des fem et des électrons de n'importe quelle centrale se
propage jusqu'à n'importe quel récepteur en moins d'1 / 1000 seconde.
2- l'éloignement du pôle nord
La force électromotrice d'attraction des électrons diminue progressivement. Des électrons s'approchent, de moins en moins nombreux.
Dans ce deuxième temps, la fem et l'intensité diminuent.
3- l'approche du pôle sud
La force devient de répulsion. Tout se passe comme lors du premier temps mais dans le sens électronique inverse. Pour marquer la différence, fem et intensité
sont déclarées négatives.
Dans ce troisième temps, la fem et l'intensité négatives diminuent.
???s En courant alternatif, la fem et la migration des électrons changent de sens. En continu, la fem maximale est appliquée en permanence et toujours dans le même sens. Quel avantage cela présente-t-il pour le courant continu ? Cela explique-t-il les tensions extêmes possibles avec le continu, > 800 kV, et son utilisation pour le transport du courant à très longue distance ?
4- l'éloignement du pôle sud
Tout se passe comme lors du deuxième temps mais dans le sens électronique inverse.
Dans ce quatrième temps, la fem et l'intensité négatives augmentent.
Alternateur
Les machines qui produisent de la fem alternative s'appellent des alternateurs.
Les courbes s'appellent des sinusoïdes.
Fem et courant sont alternativement positifs et négatifs.
Les quatre temps constituent une phase. Chaque phase dure une période, T (s). Le nombre de périodes par seconde s'appelle la fréquence, f (hertz, Hz)
La fem au temps t (s) vaut E = Emax x sin(ωt) où ω est la vitesse de rotation, vitesse angulaire, (radians / s) avec ω = 2 x π (rad) x f (Hz) =
2 x π (rad) / T (s)).
I = Imax x sin(ωt - φ) où φ (radians), notion expliquée plus loin, est le déphasage éventuel entre fem et intensité.
Pour faire varier Emax et la fem, les alternateurs utilisent des électro-aimants qui recyclent une partie du courant.
La fem de l'Union Européenne est alternative, sinusoïdale, avec f = 50 Hz et T = 1 / 50 seconde.
Courant alternatif triphasé
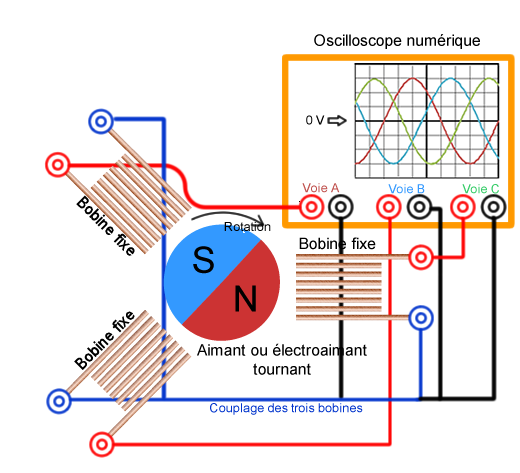
Alternateur triphasé
Par facilité de production et de transport, le courant produit par les centrales est alternatif triphasé.
En triphasé, l'aimant passe successivement devant trois bobines et engendre trois fem.
Lorsque l'aimant est devant, par exemple, la deuxième bobine, la fem y est au maximum alors qu'au
même instant celle de la première, l'aimant s'éloignant, est en train de diminuer tandis
que celle de la troisième, l'aimant s'approchant, est en train d'augmenter.
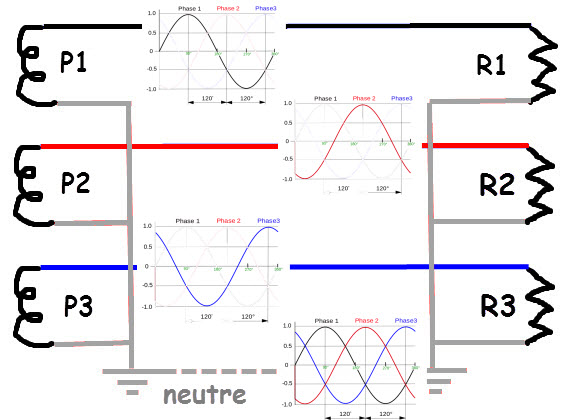
Allers séparés / retour ensemble
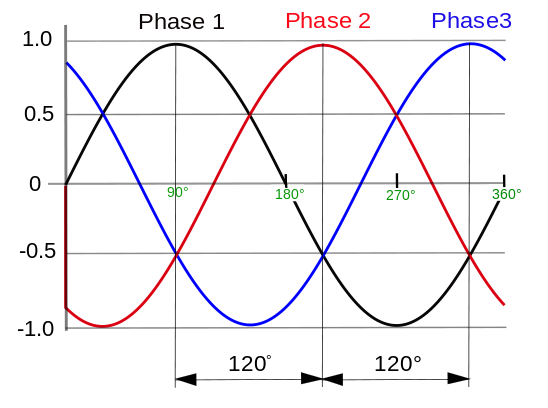
La somme des trois fems vaut toujours 0
Les trois fem sinusoïdales sont déphasées de 1 / 3 tour soit 120 ° (360 ° / 3).
Chaque fem s'appelle une phase (Pi). Sur le schéma, le fil noir reçoit P1, le fil rouge reçoit P2, le fil bleu reçoit P3, le fil gris relié à la terre (neutre) reçoit
P1 + P2 + P3.
À tout instant, la somme des trois fem est nulle, le système est équilibré, la fem du neutre est nulle, le neutre ne transporte aucun courant et est inutile. Il est ainsi
possible de remplacer le fil neutre par deux simples prises de terre et de réduire le nombre de fils du réseau à trois.
Le cumul des fem au travers d'un conducteur est une propriété essentielle à la bonne compréhension de l'électricité. Le neutre en fem triphasée en est le meilleurs exemple.
Il faut préparer son esprit à des rencontres avec d'autres cas beaucoup plus compliqués.
Noter que le courant est aussi une onde sinusoïdale et est soumis aux mêmes règles.
Explications

6 fils. Comme avec 3 générateurs indépendants
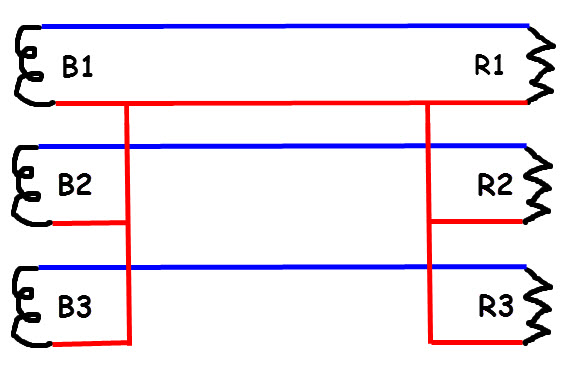
Triphasé déséquilibré
4 fils. Les circuits sont fermés grâce au fil commun,
théoriquement sans courant, le neutre
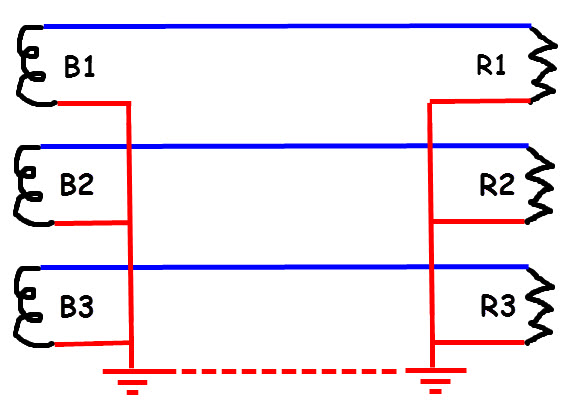
Triphasé équilibré
3 fils. Terre remplace le quatrième fil
Un seul alternateur fonctionnant comme trois, le transport d'électricité avec trois fils au lieu de six, sur des milliers de kilomètres, la facilité de transformer les fem, voir 1.7, les meilleurs rendements des alternateurs et des moteurs ainsi que de moindres pertes lors du transport expliquent l'adoption mondiale du courant alternatif triphasé.
Courant alternatif monophasé
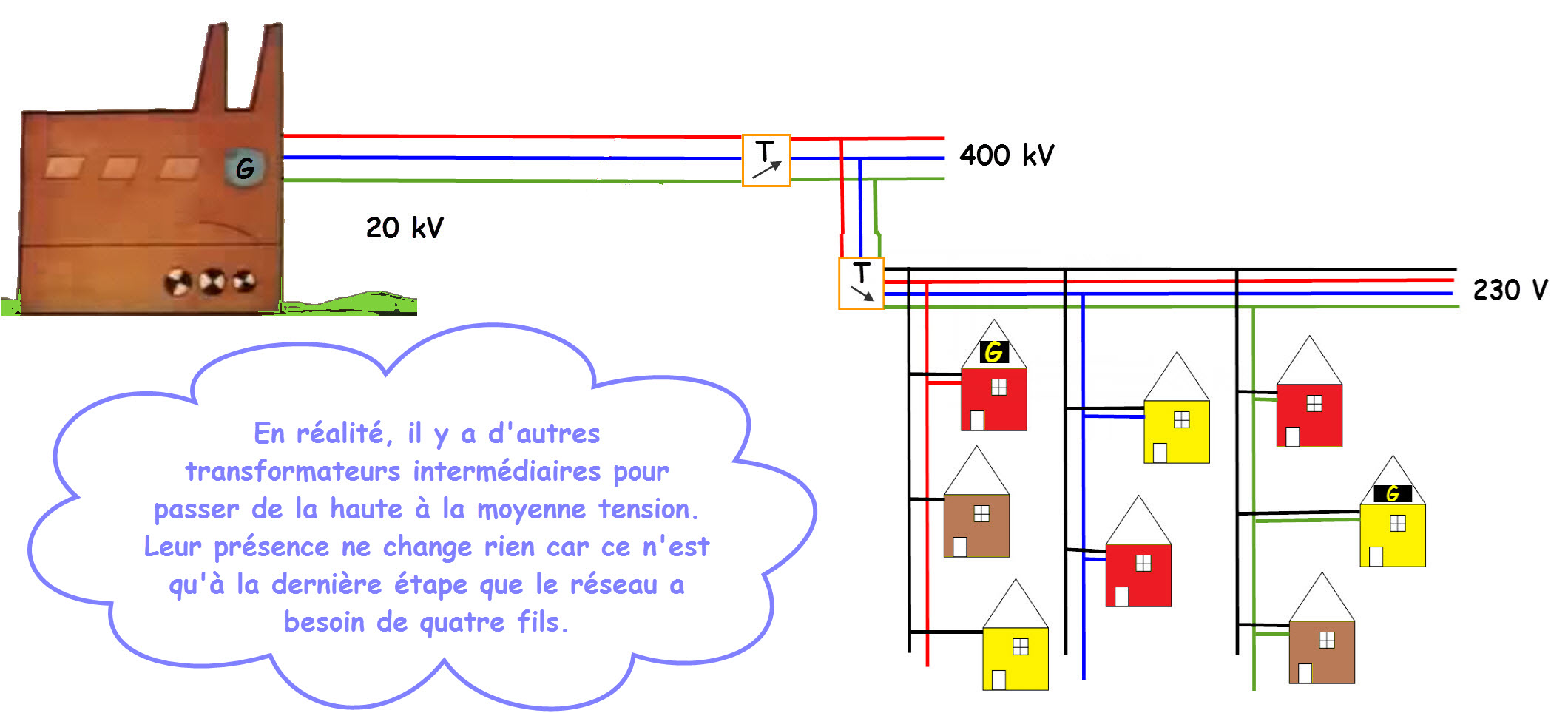
Passage du triphasé au monophasé
Le courant triphasé équilibré part de la centrale au travers de trois fils. Différents transformateurs, voir 1.7, élèvent et abaissent la fem
pour réduire les coûts de transport, voir 1.8. Le dernier transformateur est celui qui abaisse la tension à 230 V.
C'est à partir de ce transformateur que le courant est distribué aux installations. Chacune est raccordée à une phase, d'où l'appellation monophasée, et au neutre.
Il existe aussi la possibilité de raccorder certaines installations à deux phases afin qu'elles disposent d'une tension de 400 V.
Dans ces deux configurations le neutre transporte de l'électricité et est relié au neutre "équilibré" et à la terre au niveau du dernier transformateur.
Quatre ou six conducteurs sont nécessaires dans la partie distribution.
???p en quoi consiste une installation triphasée ? Que permet-elle ?
Courant continu
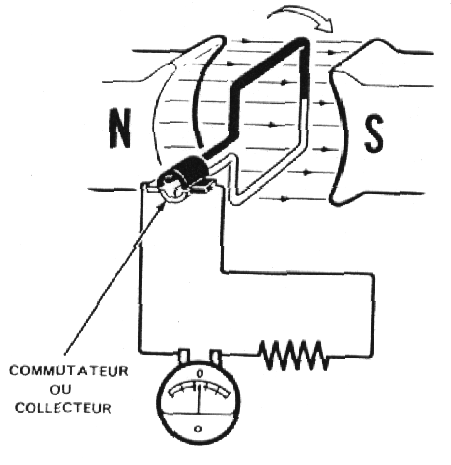
Le collecteur est en deux parties.
Chaque demi tour les fils sont inversés et le courant ne devient jamais négatif.
Les quatre étapes sont approche du pôle nord, éloignement du pôle nord,
approche du pôle nord, éloignement du pôle nord.
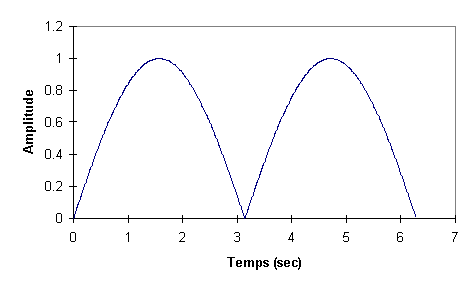
Voici la fem avec une seule spire.
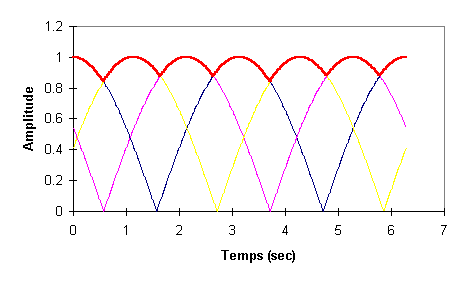
La multiplication des spires permet d'obtenir une fem continue.
Pour ne conserver que le haut de la courbe, il faut réduire le
collecteur.
Avec trois spires le collecteur couvre 2 x 60 °

(travail, énergie, joule, puissance, watt, kilowattheure)
Qu'est la puissance ?
Sa compréhension est indispensable car son unité de mesure, le watt (W), est inscrite sur tous les appareils élecriques, lampe de 100 W, aspirateur de 2000 W ...
Elle caractérise également les générateurs d'électricité.
Une force, la fem, qui déplace son point d'application, l'électron, fournit un travail ou énergie.
La manifestation de ce travail est la chaleur ou le champ magnétique.
Les électrons qui migrent dans un corps, sous l'action de la fem, fournissent un travail et transmettent de l'énergie.
Le travail et l'énergie sont mesurés en joules (J).
La puissance du générateur est la quantité d'énergie électrique qu'il produit chaque seconde. Celle du récepteur, est la quantité d'énergie électrique qu'il consomme chaque
seconde. La puissance s'exprime en watts (W) (1 W = 1 J/ 1 s).
Il y a très souvent confusion entre puissance et efficacité. L'ampoule électrique de 100 W illustre bien cette confusion. L'acheteur imagine que plus elle est puissante et mieux elle éclaire. Les ampoules à basse consommation actuelles prouvent qu'il n'en est rien. La seule certitude est qu'une ampoule de 75 W consomme trois fois plus par seconde qu'une ampoule de 23 W.
Le kilowattheure (kWh) est une autre unité d'énergie. Elle représente la production d'un générateur, ou la consommation d'un récepteur, de 1 kW pendant 1 h.
1 kWh = 3.600 kJ.
La relation entre la puissance (P), le potentiel (U) et l'intensité (I) est la suivante : P (W) = U (V) x I (A).
Combinée avec la loi d'Ohm : P (W) = R (Ω) x I2 (A2).
Cette formule montre aussi que 1 W = 1 V x 1 A en plus de 1 J / 1 s.
La limite de puissance d'un raccordement est imposée par le compteur électrique qui contient un dispositif, un disjoncteur, qui coupe automatiquement le courant. Le disjoncteur d'un compteur ordinaire intervient à partir de 40 A soit 9.200 W (230 V x 40 A) . Il est donc impossible d'aller au delà.
Un alternateur est caractérisé par sa puissance nominale et sa puissance maximale.
La puissance nominale est celle qu'il fournit au circuit sans effort particulier. La puissance maximale est celle qu'il ne faut pas dépasser sous peine
d'endommagement.
Quelques puissances nominales : installation photovoltaïque domestique 5 kW, éolienne terrestre 2 à 5 MW, barrage 420 MW, réacteur nucléaire 900 à 1650 MW.
Il s'agit, en ce début de recherche, de la loi de puissance originelle. Elle est applicable dans la majorité des cas.
Tous les cas possibles sont couverts par la loi de puissance généralisée et l'impédance. Ces notions sont abordées plus loin.
(lois de Kirchhoff)
Dans la pratique, tous les circuits sont mixtes. Les récepteurs sont en parallèles mais sont reliés par des conducteurs en série.
Exemple illustré : une batterie de 12 V, un fil de 2 m, une prise multiple avec, d'une part, un fil de 8 m et une lampe de 4 Ω et, d'autre part, un fil de 10 m et deux lampes de
6 Ω.
Ne pas oublier que il y a deux fils dans chaque "fil". Résistance de 0,1 Ω / m de fil.
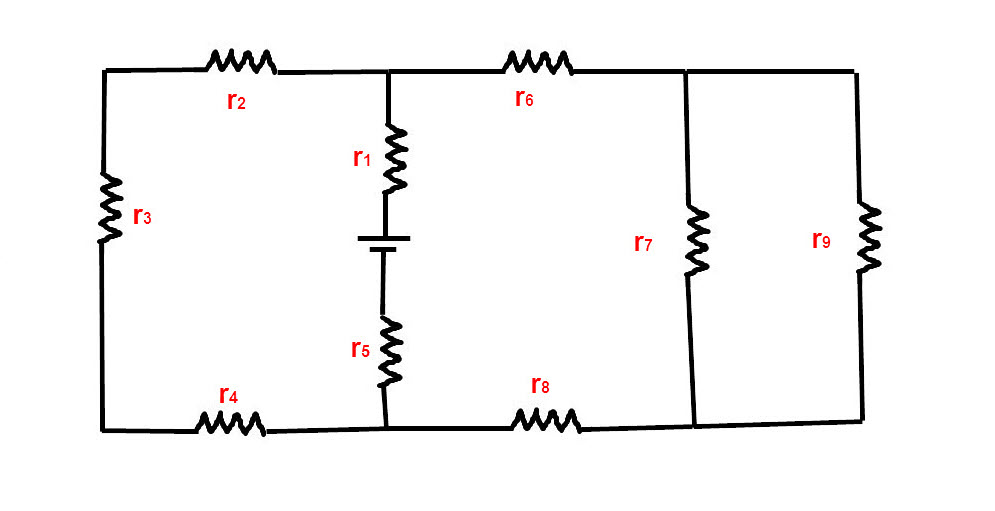
1° Dessiner le circuit.
U = 12 V.
Rr1 = Rr5 = 0,2 Ω.
Rr2 = Rr4 = 0,8 Ω.
Rr3 = 4 Ω.
Rr6 = Rr8 = 1 Ω.
Rr7 = Rr9 = 6 Ω.
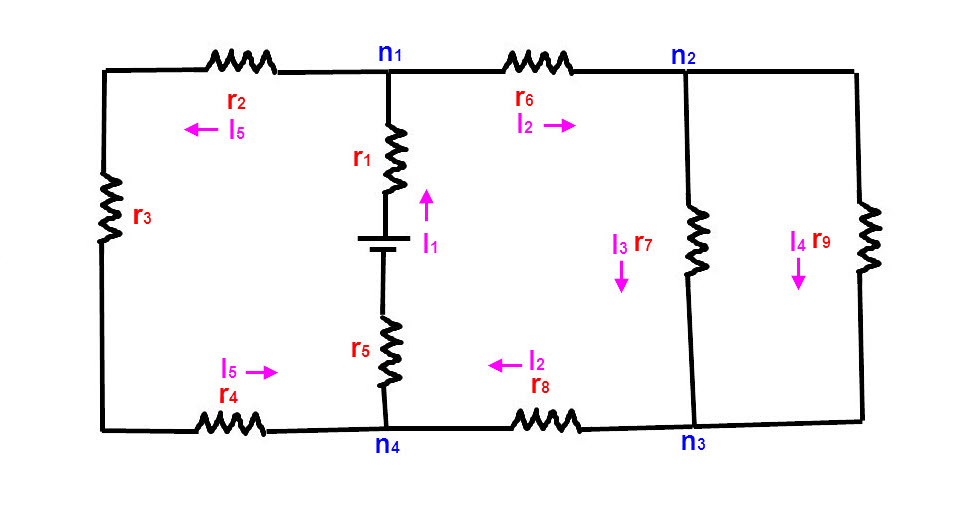
2° Identifier les noeuds, ni, les courants, Ii et leur sens.
Le choix du sens est libre. Choisir un sens logique.
Limiter le nombre des courants.
Par exemple, Ir6 = Ir7 + Ir9 = Ir8.
Pour simplifier, autant appeler les deux I2.
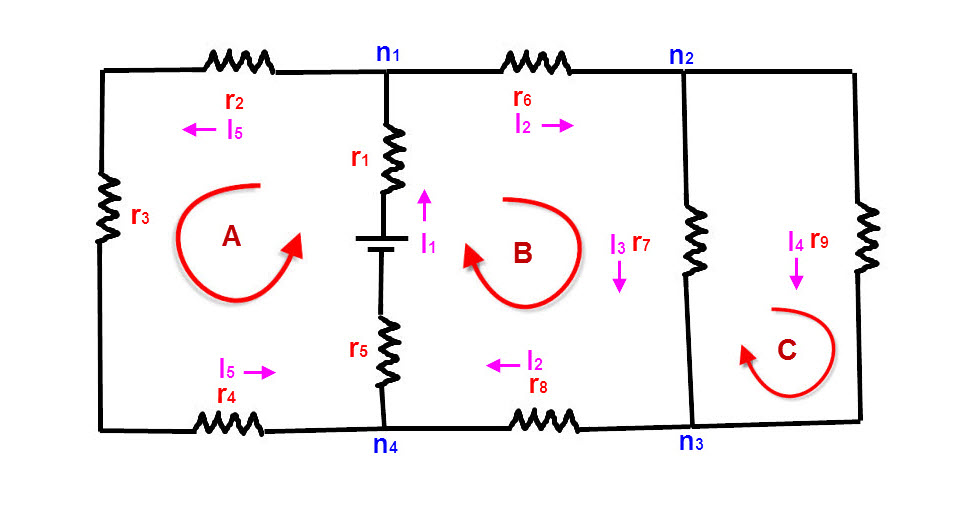
3° Identifier les boucles et leur sens.
Le choix du sens est libre. Choisir un sens logique.
Le nombre de boucles est libre. Pourquoi en choisir six lorsque trois suffisent.
4° Appliquer la loi des boucles de Kirchhoff.
La somme des ddp (V) d'une boucle égale 0.
La fem est positive si la boucle va de - vers + et inversément.
La ddp d'une résistance ri vaut Rri x Ii. Elle est négative si la boucle va dans le sens du courant et inversément.
La boucle C en est un bon exemple.
Boucle A :
12 - 0,2 I1 - 0,8 I5 - 4 I5 - 0,8 I5 - 0,2 I1 = 0
Boucle B :
12 - 0,2 I1 - 1 I2 - 6 I3 - 1 I2 - 0,2 I1 = 0
Boucle C :
6 I3 - 6 I4 = 0
5° Appliquer la loi des noeuds de Kirchhoff.
La somme des intensités (A) d'un noeud égale 0.
L'intensité est positive si le courant entre dans le noeud et inversément.
n1 et n4 :
I1 - I2 - I5 = 0
n2 et n3 :
I2 - I3 - I4 = 0
6° Résoudre le système d'équations.
Il faut disposer de n équations linéaires à n inconnues. Les simplifier et les organiser en deux matrices. Les variables dans la première et les constantes dans l'autre.
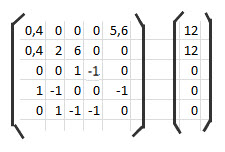
Représentation matricielle
de 5 équations à 5 inconnues
0,4 I1 - 0 I2 - 0 I3 - 0 I4 + 5,6 I5 = 12
0,4 I1 + 2 I2 + 6 I3 - 0 I4 - 0 I5 = 12
0 I1 + 0 I2 + 1 I3 - 1 I4 - 0 I5 = 0
1 I1 - 1 I2 - 0 I3 - 0 I4 - 1 I5 =0
0 I1 + 1 I2 - 1 I3 - 1 I4 - 0 I5 =0
La méthode est excellente mais les signes sont un cauchemar.
Pour résoudre ce genre d'équation, utiliser les fonctions inversemat et produitmat de Excel sans oublier ctrl + maj + entrée (https://www.youtube.com/watch?v=gSNa3fQX0WQ).
Pour faciliter la saisie dans le tableur, préparer les équations sous forme "matricielle".
Les intensités connues, calculer les ddp, V = R x I, puissances, P = U x I et énergies, W = P x Δt.
Les lois de Kirchoff, d'Ohm et de Joule permettent de répondre à de très nombreuses questions. En voici quelques unes.
Comment intégrer la fem E variable dans les calculs ?
Les piles et les batteries ont une fem E constante. Par contre, les générateurs peuvent faire varier E pour garder la tension U constante. Comment le modéliser et
le calculer ?

Ex. 1 : E = 12 V
Ex. 2 : U = E - Vg = 12 V
Commentaire : U = Vr = 12 V
Exemple 1
Avec une batterie de E = 12 V et des résistances d'1 Ω, la boucle nous donne :
12 - 1 I1 - 1 I1 - 1 I1 - 1 I1 = 0 donc 12 - 4 I1 = 0 donc I1 = 3 A.
Vg = 12 V - 9 V, Vc1 = 9 V - 6 V, Vr = 6 V - 3 V et Vc2 = 3 V - 0 V.
Exemple 2
Avec un générateur de U = 12 V et des résistances d'1 Ω, la boucle nous donne :
1 E - 1 I1 - 1 I1 - 1 I1 - 1 I1 = 0 donc 1 E - 4 I1 = 0. 1 E remplace 12. Avec une inconnue de plus, il faut une équation de plus.
U = E - 1 I1 = 12 V.
1 E - 4 I1 = 0
1 E - 1 I1 = 12
I1 = 4 A
U = 16 - 4 = 12 V
Vc1 = 12 V - 8 V, Vr = 8 V - 4 V et Vc2 = 4 V - 0 V.
Pour intégrer E variable, ce qui ajoute une inconnue, il suffit d'ajouter l'équation de calcul de la tension U = E - (Rg x I).
La définition de la tension U, et sa formule de calcul, est très souple.
Supposons que U soit la tension fournie au récepteur U = Vr = E - ((Rg + Rc1 + Rc2) x I) = 12 V.
Dans ce cas, I = 12 A, 3 I = E - 12 et E = 48 V. Vg = 48 V - 36 V, Vc1 = 36 V - 24 V, Vr = 24 V - 12 V et Vc2 = 12 V - 0 V.
Ça marche, même avec des matrices, à condition d'être précis.
Comment ne pas dépasser la limite de puissance d'un générateur ?
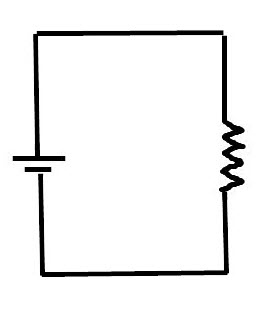
U = 12 V
Pmax = (E x I)max = 144 W
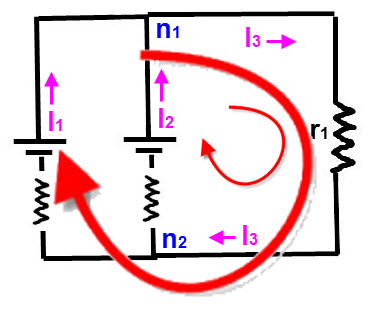
Le courant peut être réparti entre
des générateurs en parallèle
Tout générateur a une puissance maximale Pmax = (E x I)max.
I augmente avec le nombre de récepteurs, voir ci-dessus. À tension constante, E augmente avec I, voir ci-dessus. À un moment, la limite de puissance peut être dépassée.
Que faire ?
Exemple : U = 12 V, Pmax = 144 W. R = 1 Ω.
Avec la seule boucle de droite,
1 E - 1 I2 - 1 I3 = 0
1 I2 - 1 I3 = 0
1 E - 1 I2 = 12
I = 12 A,E = 24 V, P = 24 x 12 = 288 W. La limite de 144 W est franchie et le circuit en danger.
Avec un second générateur en parallèle, donc avec deux boucles,
boucle 1,
1 E - 1 I1 - 1 I3 = 0
boucle 2,
1 E - 1 I2 - 1 I3 = 0
noeud 1,
1 I1 + 1 I2 - 1 I3 = 0
équation de calul de U,
1 E - 1 I1 = 12
1 E - 1 I2 = 12
I1 = I2 = 6 A, I3 = 12 A,E = 18 V, P = 18 x 6 = 108 W. Les limites de 144 W sont infranchies et le circuit sans danger.
Le courant est réparti entre les générateurs en parallèle. Pour chaque générateur, moins d'intensité entraîne moins de fem et moins de puissance.
Une centrale compte plusieurs générateurs en parallèle. Un générateur assure la base et les autres sont utilisés en renfort.
Si nécessaire, utiliser l'artifice du r pour résoudre le système d'équations. Penser que, même infiniment petite, il y a toujours une résistance. si elle est inconnue, il faut la représenter par une lettre, r par exemple.
D'où vient le courant lorsque les générateurs se trouvent sur différents sites ?

Eg1 = Eg2, U = 12 V, Rr1 = 1 Ω
G1 à 30 m (Rg1 = 3 Ω), G2 à 10 m (Rg2 = 1 Ω)
Supposer dans ce cas que la fem est constante et la tension variable.
1 E - 3 I1 - 1 I3 = 0
1 E - 1 I2 - 1 I3 = 0
1 I1 + 1 I2 - 1 I3 = 0
1 E - 1 I2 = 12
E = 21 V
I1 = 3 A, I2 = 9 A, I3 = 12 A
U = 21 - (3 x 3) = 21 - (1 x 9) = 12 / 1 = 12 V
Pg1 = 21 x 3 = 63 W, Pg2 = 21 x 9 = 189 W
PRg1 = 3 x 32 = 27 W, PRg2 = 1 x 92 = 81 W, Pr1 = 12 x 12 = 144 W
Pg1 + Pg2 = 252 W = PRg1 + PRg2 + Pr1
La puissance générée égale la puissance consommée.
3 I1 = 1 I2. Le courant est réparti en proportion inverse de la résistance, donc de la distance.

Ug1 = 12 V, Rg1 = 3 Ω, Ug2 = 12 V, Rg2 = 1 Ω, Rr1 = 1 Ω
1 E1 - 3 I1 - 1 I3 = 0
1 E1 - 3 I1 = 12
1 E2 - 1 I2 - 1 I3 = 0
1 I1 + 1 I2 - 1 I3 = 0
Avec un système de 4 équations à 5 inconnues, il faut supposer des valeurs d'une variable et observer comment évoluent les valeurs des autres.
Une seule variable est connue. I3 = 12 A. En découle I1 + I2 = 12. Cette équation est très intéressante car, lorsqu'une intensité est négative, elle indique un
contre-courant, une traversée catastrophique d'un générateur par le courant de l'autre.
Faire varier E1 ou E2 permet de déterminer les limites de fem des deux générateurs. Choisir E1 ne change rien à l'analyse, tant les quatre variables sont liées.

Ug1 = 12 V, Rg1 = 3 Ω, Ug2 = 12 V, Rg2 = 1 Ω, Rr1 = 1 Ω
Pour assurer une tension de 12 V, E1 doit valoir entre 12 V et 48 V et E2 entre 12 V et 24 V. En dehors de ces valeurs le générateur le plus faible est traversé
par le courant généré par le générateur le plus fort.
Noter que la limite inférieure, E = 12 V, correspond à la tension U = 12 V avec un courant egal à 0, comme l'indique les cellules vertes du tableau.
Si les tensions sont inégales, il se produit un contre-courant, une traversée catastrophique d'un générateur par le courant de l'autre.
Le signe négatif de I1, ou de I2, indique que le courant réel circule dans le sens inverse de celui du schéma.
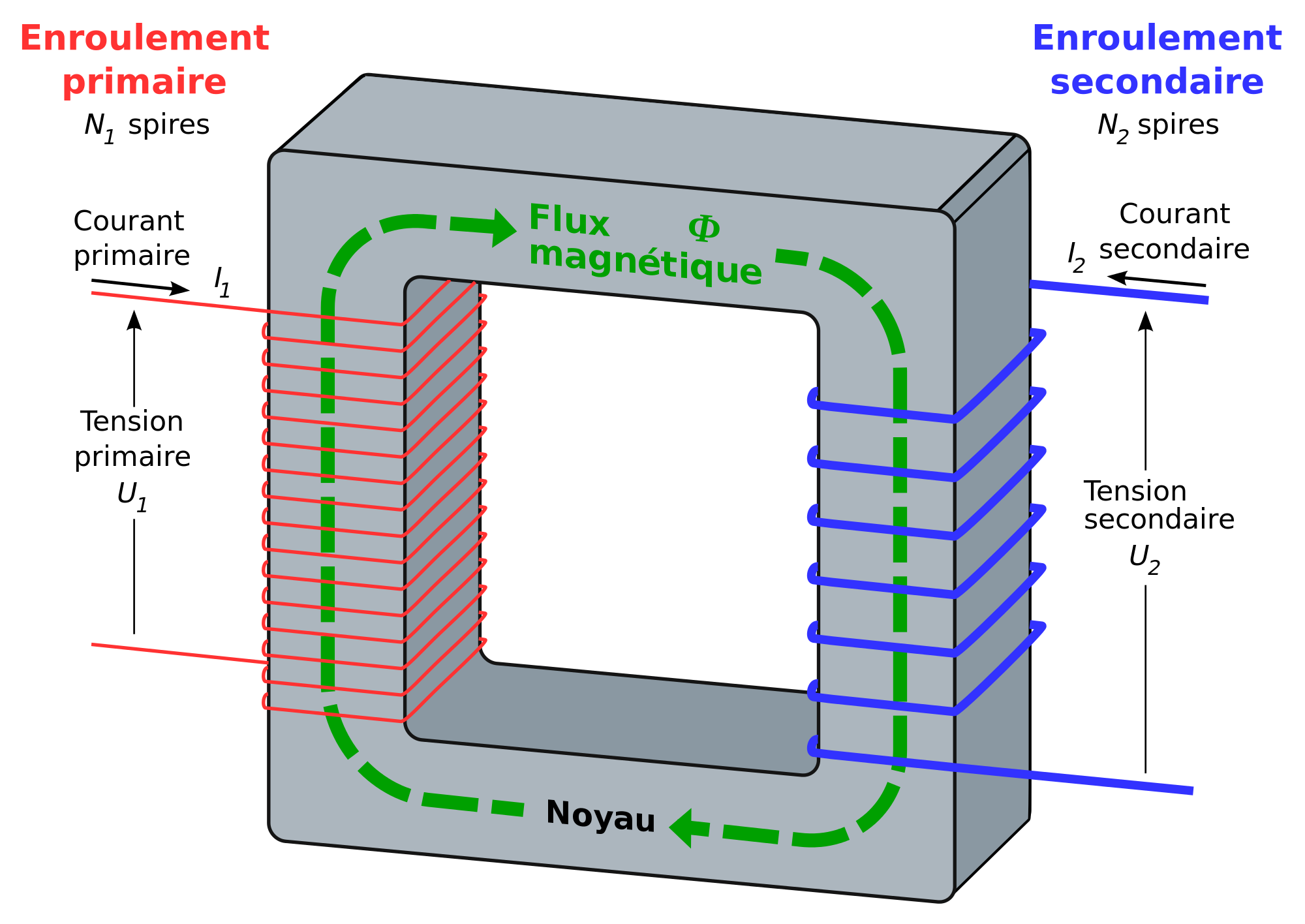
Schéma d'un transformateur
Le transformateur transforme le courant alternatif d'une source en un courant de même fréquence, de même forme mais de tension différente.
Un transformateur est constitué par deux bobinages reliés par une armature ferromagnétique.
Premier temps : le courant fourni par la source induit dans le bobinage primaire un champ magnétique.
Deuxième temps : l'armature transporte ce champ magnétique jusqu'au bobinage secondaire.
Troisième temps : le champ induit un courant dans le bobinage secondaire.
Transformateur idéal
Un transformateur idéal est un transformateur virtuel sans aucune perte.
Dans ce cas, les puissances sont égales. P1 = U1 x I1 = P2 = U2 x I2.
Selon la loi d'Ohm, R1 = U1 / I1 et R2 = U2 / I2.
Il est aussi possible de calculer R1 en fonction de R2 grâce à la formule R1 = R2 x (U1 / U2)2.
R1 / R2 = (U1 / I1) / (U2 / I2) = (U1 / I1) x (I2 / U2) = (U1 / U2) x (I2 / I1) = (U1 / U2)2
Attention, la formule risque de provoquer une importante erreur d'arrondi. Il vaut mieux utiliser la loi d'Ohm.
Dans un transformateur idéal, le rapport des tensions égale le rapport des nombres de spires.
Le rapport de transformation m = U2 / U1 = N2 / N1 où Ni est le nombre de spires du circuit i.
Comprendre que, pour une fem donnée, la tension est fonction du nombre de spires. Cette règle est valable aussi pour les alternateurs.

Pylônes à haute tension
La haute tension apporte la solution pour le transport de très grandes puissances à l'aide de conducteurs techniquement et économiquement fabricables.
Les changements de tension nécessaires sont réalisés à l'aide de transformateurs capables d'élévations et d'abaissements.
Plus la tension est élevée et plus le diamètre du câble est petit
Supposer que la perte acceptable par effet de Joule est limitée à 5 % de la puissance fournie aux habitations.
Conducteur 1 (C1, 10 km, cuivre, P1 = 12.500 W) + habitations (P2 = 500 kW) + conducteur 2 (C2, 10 km, cuivre, P3 = 12.500 W).
| Calcul | U1 = 230 V | U2 = 20 kV |
| P = P1 + P2 + P3 | 525 kW | 525 kW |
| I = I1 = I2 = I3 = P / U | 525 kW / 230 V = 2283 A | 525 kW / 20 kV = 26 A |
| RCn = Pn / I2 | 12.500 W / 22832 A2 = 0,002 Ω | 12.500 W / 262 A2 = 18,491 Ω |
| SCn = ρ x L / RCn | 17.10-9 Ω.m x 10 km / 0,002 Ω = 0,085 m2 = 850 cm2 | 17.10-9 Ω.m x 10 km / 18,491 Ω = 9.10-6 m2 = 9 mm2 |
| DCn = 2 x √ (SCn / π) | 2 x √ (850 cm2 / 3,14159) = 33 cm | 2 x √ (9 mm2 / 3,14159) = 3 mm |
Les chiffres parlent d'eux-mêmes.
Pour éviter des câbles de 30 cm, voire plus, la tension est élevée au maximum.
Chaque niveau d'un pylone supporte une phase. Chaque phase est constituée de un à quatre conducteurs. Un ensemble de trois phases s'appelle un terne. Les pylones supportent
jusqu'à huit ternes. Le câble au sommet est un paratonnerre qui peut aussi supporter une fibre optique, pour transmettre des informations.
Sur la photo, chaque pylone supporte quatre ternes avec deux conducteurs par phase.(???p à vérifier)
Tensions en Wallonie : hautes, 380, 220, 150, 70, moyennes 30, 15 kV, basses, 400 et 230 V.
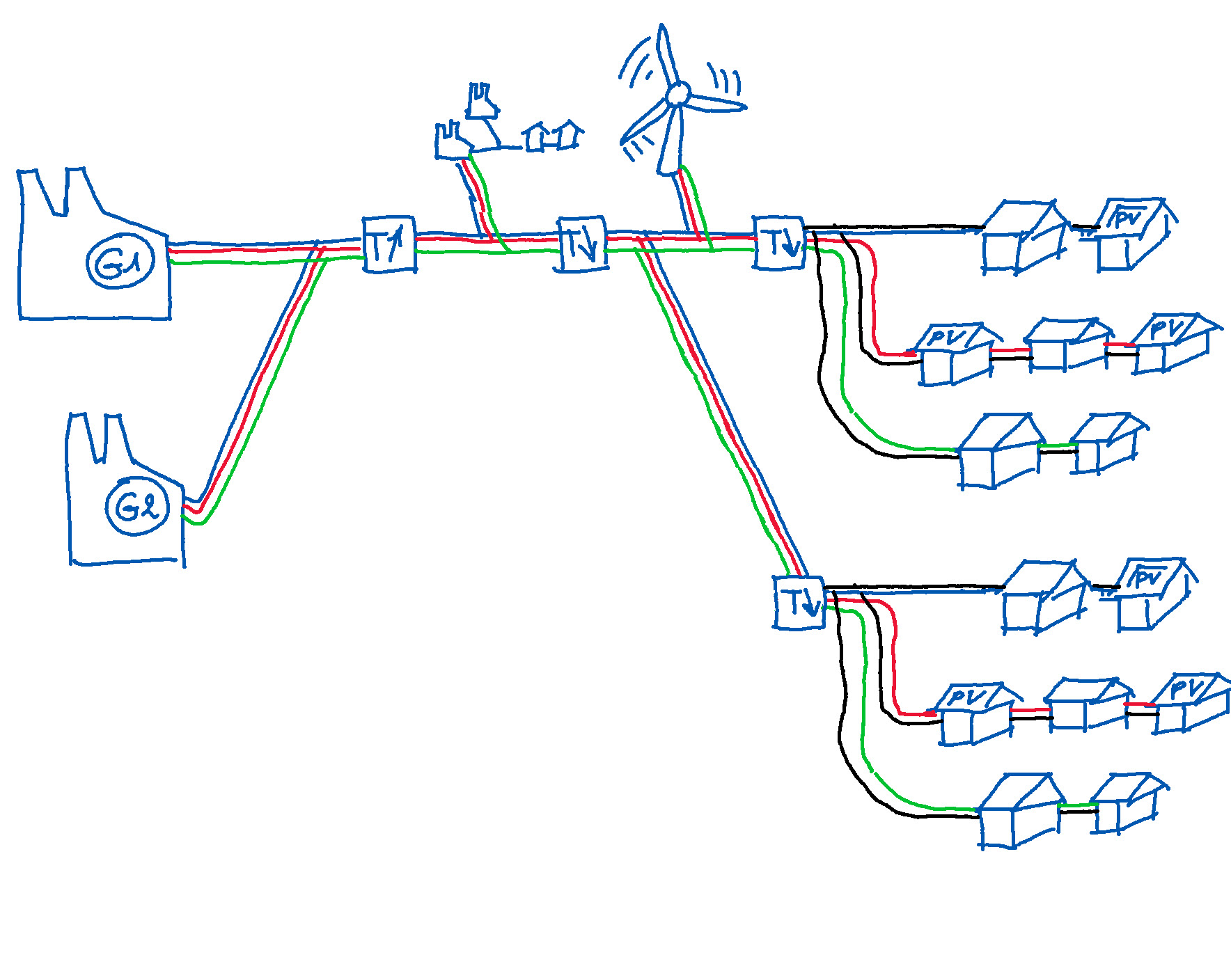
Réseau décentralisé de transport et de distribution d'électricité
Un réseau est un circuit mixte. Dans un réseau, générateurs, raccordements et récepteurs sont raccordés en parallèle à des conducteurs raccordés en série.
Les générateurs interconnectés à la même tension délivrent ensemble toute la puissance nécessaire
car les puissances consommées sont réparties entre eux.
Les centrales produisent un courant triphasé équilibré. Trois conducteurs suffisent pendant tout le trajet. Au départ et à l'arrivée, un conducteur
commun, le neutre, est raccordé à la terre.
Le courant est transporté à différentes tensions, haute, moyenne et basse, afin d'optimiser les sections de câbles.
Les transformateurs assurent les changements de tension.
Il y a trois parties dans un réseau. Le transport, avec des générateurs puissants, des transformateurs et des lignes à haute tension. La répartition, avec
peu de générateurs, des tranformateurs et des lignes à haute et moyenne tension. La distribution avec des tranformateurs et des lignes à basse tension.
Le plus souvent, le transport est un réseau maillé, avec des redondances de sources. La répartition est maillée ou bouclée, avec des artères alimentées par
deux sources situées aux extrémités. La distribution est une arborescence depuis un poste source vers des transormateurs MT/BT et, ensuite, vers des
consommateurs.
Dans la partie de distribution du réseau, 230 V, trois zones, qualifiées de monophasées, sont raccordées, par quatre ou six conducteurs à une phase et au conducteur
commun, le neutre. Il existe aussi la possibilité de raccorder certaines installations à deux phases afin qu'elles disposent d'une tension de 400 V. Certaines
autres installations reçoivent les trois phases. Voir détails au chapitre 2. (???p)
De plus en plus de réseaux sont interconnectés et échangent du courant.
Les réseaux centralisés, avec une seule source de courant alimentant tout une arborescence de raccordements, disparaissent. Ils sont remplacés par des
réseaux décentralisés avec une multitude de producteurs, connectés à différents niveaux de tension.
Le nombre de conducteurs varient d'un continent à l'autre. Trois phases et neutre en Amérique, trois phases seules en Europe, monophasé à un seul conducteur en Australie.
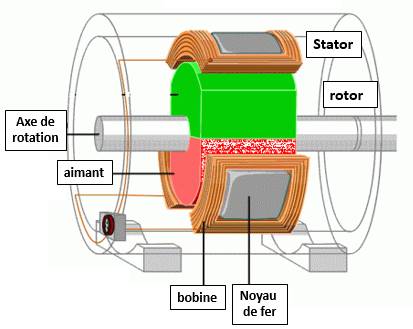
Schéma d'un alternateur
L'essentiel de l'électricité mondiale est produite par des alternateurs.
En supposant que l'effet du courant induit par une tension de 230 V est le même que celui du courant induit par une tension de -230 V, ces tensions n'apparaissent que 200 fois
par seconde, presque jamais. Dès lors, comment peut-on déclarer que la tension en U.E. est de 230 V ?
230 V est la tension efficace (Ueff (V)). La valeur efficace
d'une tension sinusoïdale vaut la tension continue qui produirait le même
échauffement
L'effet de Joule, loi de Joule, détermine l'échauffement : P (W) = R (Ω) x I2 (A2).
La loi d'Ohm détermine l'intensité : U (V) = R (Ω) x I (A).
dans une résistance.
La tension efficace est une valeur qui permet d'utiliser la loi d'Ohm (U = R x I), la formule de puissance (U = P / I), et beaucoup d'autres, avec un courant alternatif, malgré
que la tension change à tout moment.
Par exemple, un projecteur de 1000 W sous une tension efficace de 230 V consommera 1 kWh par heure. En réalité, la puissance de 1000 W, la consommation de
1000 J/s, n'existe réellement que 200 fois au cours d'une seconde, soit presque jamais. Tout le reste du temps la puissance réelle, la consommation réelle par
seconde, est plus grande ou plus petite. Cependant, comme s'il s'agissait d'une moyenne, l'énergie consommée en une heure est bien égale à 1 kWh.
En d'autres mots, la tension efficace est l'équivalente en courant continu de la tension alternative utilisée.
Ueff = Umax / √2. En U.E., Umax vaut Ueff x √2 = 230 V x 1,4142 = 325 V.
Ieff = Imax / √2
Du fait du déphasage de 120°, un réseau dont la tension efficace entre phase et neutre est de 230 V aura une tension de
Ueff x √3 = 230 V x 1,7321 = 398,37 V efficaces entre phases.
Autre avantage du triphasé, pouvoir proposer plus de puissance grâce à une tension voisine de 400 V entre phases.
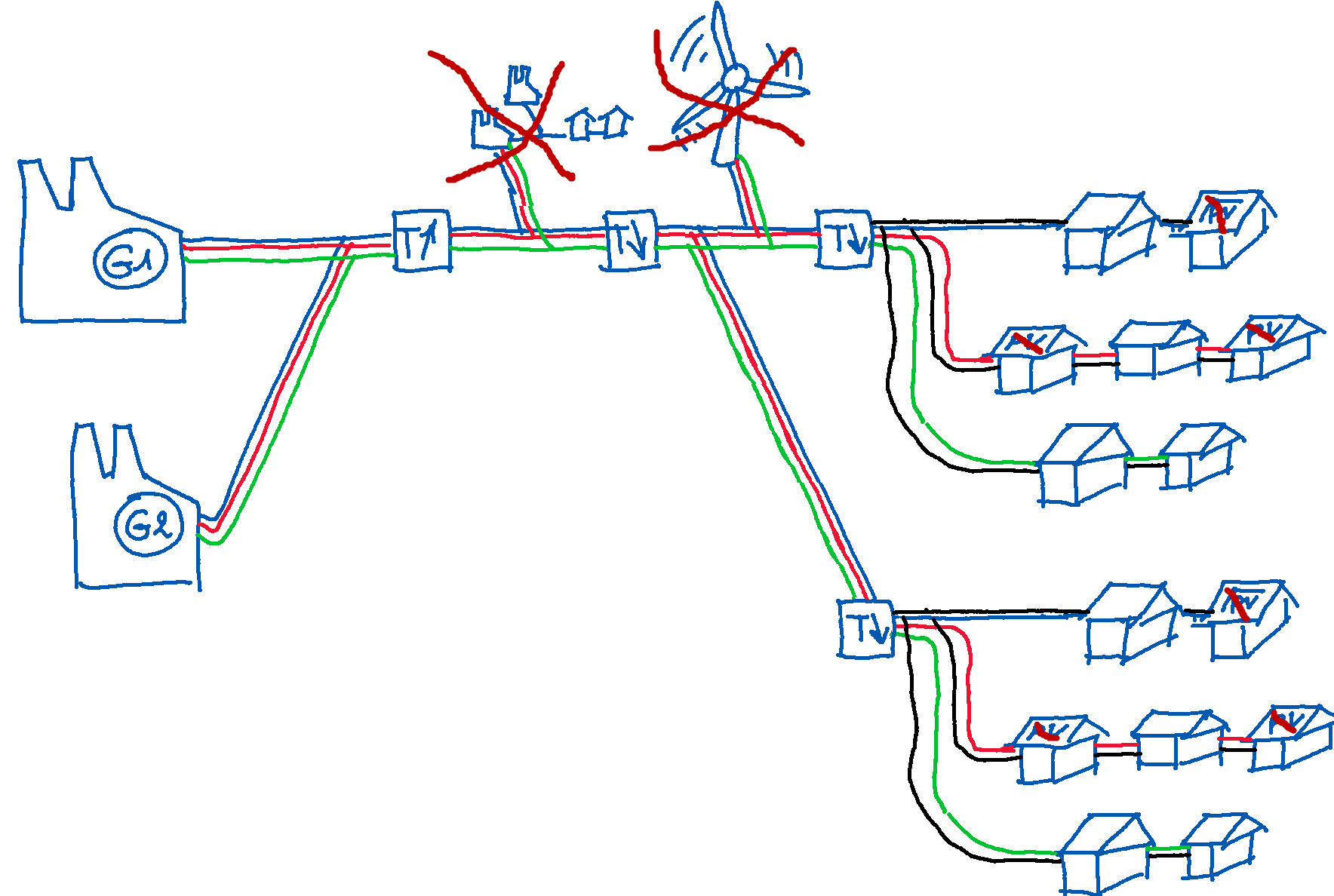
Exemple chiffré
Les deux générateurs suffisent pour 7.000 utilisateurs
Le réseau décrit n'est peut-être pas réaliste mais les résistances et les puissances sont plausibles.
Rien de tel qu'un exemple chiffré pour faire le point.
Distribution, BT
Il faut électrifier deux villages, Hausart et Bassart, en 230 V, monophasé.
Chaque village compte 3500 habitations (hab) réparties en 700 immeubles de 5 habitations.
Hausart-Nord (1000 hab) et Bassart-Nord (1000 hab) sont branchés sur la phase 1.
Hausart-Centre (1500 hab) et Bassart-Centre (1500 hab) sont branchés sur la phase 2.
Hausart-Sud (1000 hab) et Bassart-Sud (1000 hab) sont branchés sur la phase 3.
La puissance utile maximale / hab, 230 V x 40 A, égale 9200 W, soit 32,2 MW par village.
Chaque village comte 140 x 0,1 km de lignes. Chaque ligne alimente 25 hab et a une résistance de 0,15 Ω / km.
Transport, HT
Lignes 220 kV. G1 > T1, 10 km, 0,08 Ω / km. G2 > T2, 20 km, 0,08 Ω / km. Les deux lignes se rejoignent à T1.
Lignes 380 kV. T1 > T2, 100 km, 0,03 Ω / km.
Lignes 30 kV. T2 > T3, 10 km, 0,15 Ω / km. T2 > T4, 20 km, 0,15 Ω / km. Les deux lignes se séparent dès T2.
Génération
Deux générateurs G1 et G2 sont prévus. Tension 15000 V, triphasé. Ils sont raccordés directement aux lignes de transport à 220 kV, jusqu'à T1.
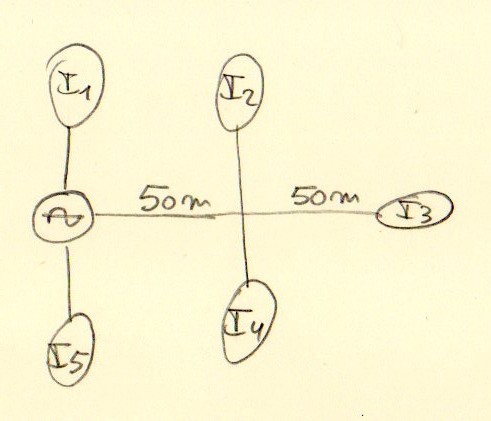
Chaque ligne de 100 m dessert 5 immeubles
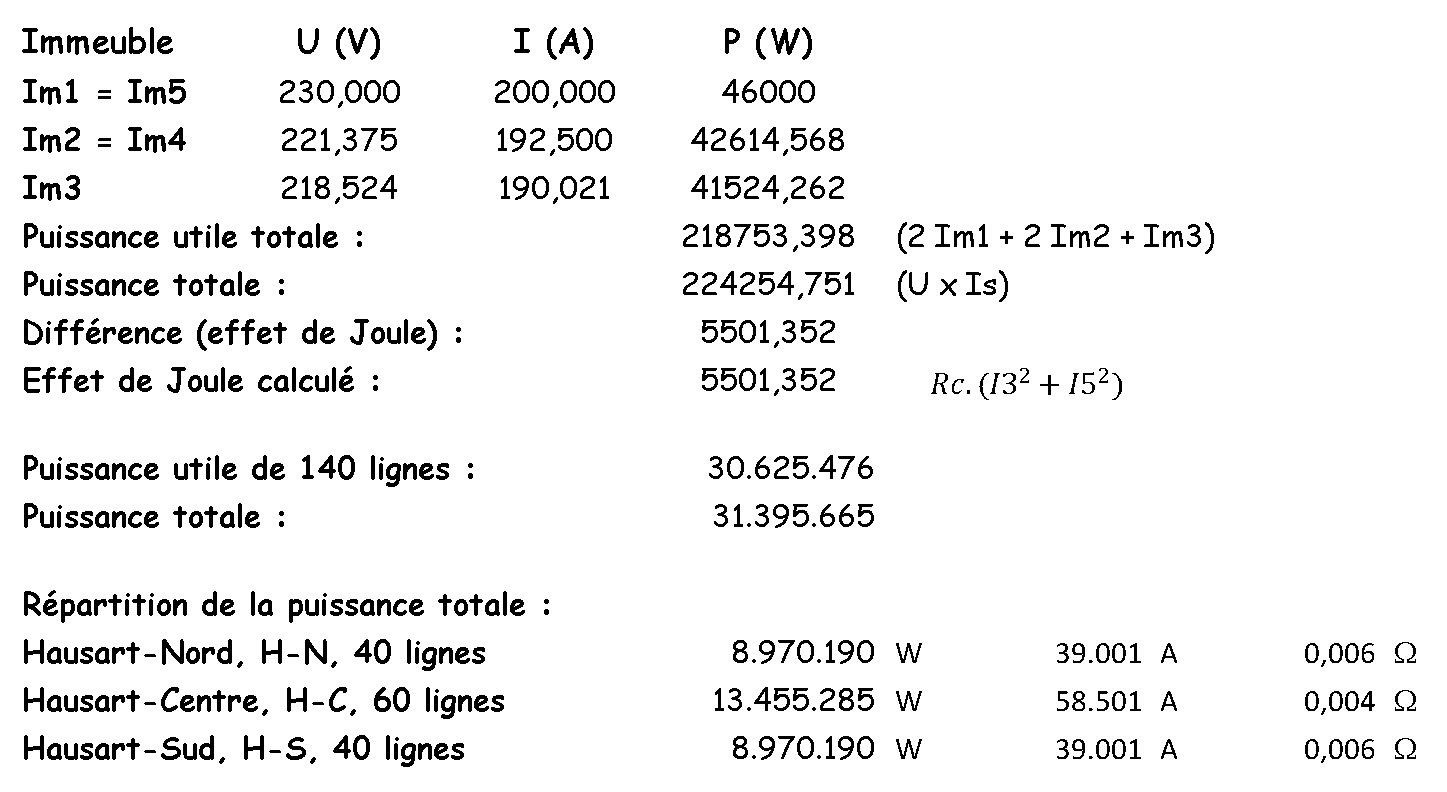
Tensions et puissances
Une tension de 230 V au transformateur assure une tension suffisante à tous les immeubles tout en limitant la puissance totale.
Les lois de Kirchhoff, Ohm et Joule, expliquées dans ce chapitre, permettent de calculer I, V et P.
Le calcul des tensions de départ, afin que chaque utilisateur dispose de 230 V ± 10 % est très complexe. V = R x I fait intervenir l'intensité et
l'intensité augmente quand le nombre d'utilisateurs augmente. Sur n'importe quelle ligne, il existe un nombre d'utilisateurs, et donc une
intensité, à partir duquel le respect de la norme devient impossible.
L'autre problème qui apparaît dès à présent est celui de l'équilibre des phases. H-C et B-C nécessitent des puissances très supérieures à celles des autres quartiers.
Équilibrer la répartition des lignes, 3 x 47, ne résoud pas le problème car la consommation est très variable dans le temps et le déséquilibre est permanent.
Lignes à haute tension, HT
Les utilisateurs BT ont des besoins libres et différents. Par conséquent, les intensités BT entre phases diffèrent sans contrôle. Comment, dans ces conditions,
un circuit triphasé équilibré, où les tensions doivent être égales, peut-il fonctionner ?
Par manque d'info. faire comme s'il y avait 3 circuits.
Comme il y a deux villages, il y a donc six circuits à calculer.

La production de six générateurs est transportée vers Hausart
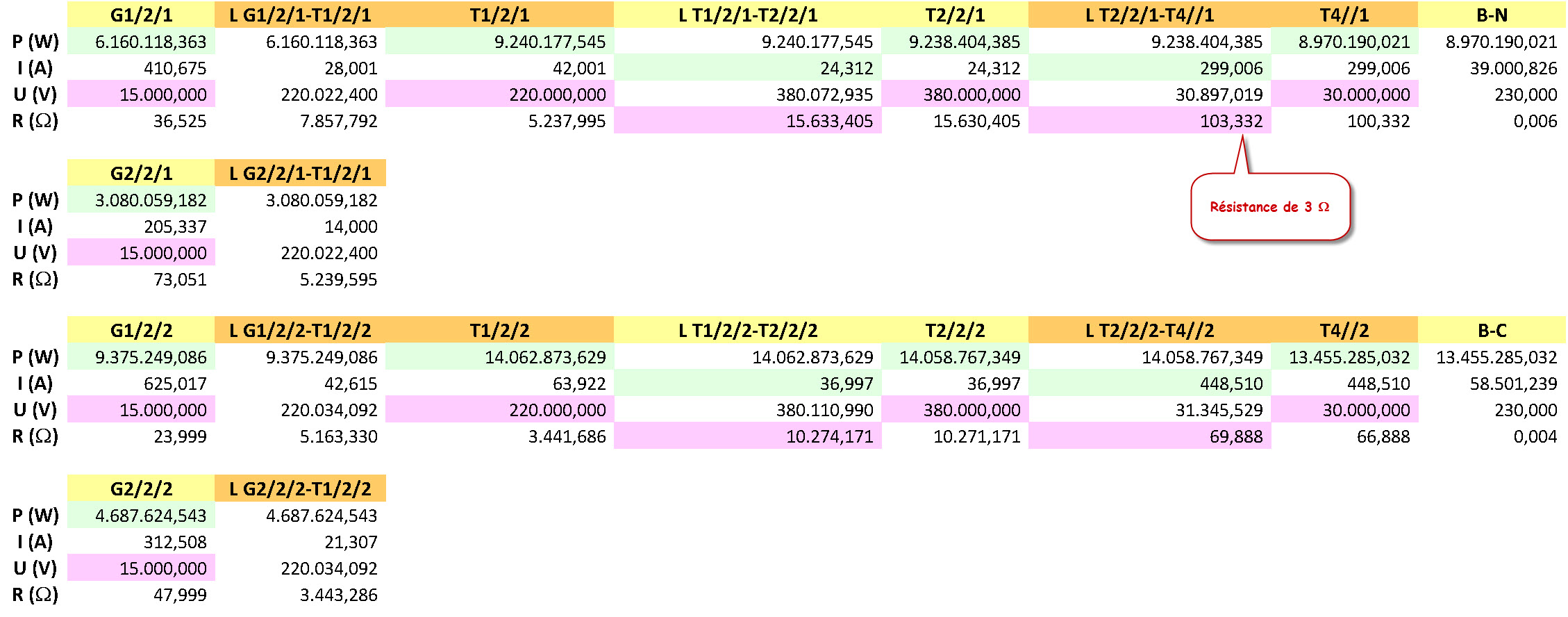
La production de six générateurs est transportée vers Bassart
Cet exercice montre que les bases sont suffisantes pour faire des calculs en monophasé mais insuffisantes, faute de règles d'équilibrage des phases et de transformation, pour les
calcul en triphasé.
En attendant, le résultat est constitué de 6 circuits au lieu d'un seul, 12 générateurs au lieu de 2, 24 transformateurs au lieu de 6.
A présent, le problème d'équilibrage des phases apparaît clairement. Les tensions entre phases diffèrent, ce qui est contraire au principe.
Les techniques d'équilibrage sont décrites dans les chapitres suivants. En attendant, ces contraintes ne sont pas prises en compte et les calculs sont réalisés comme s'il
s'agissait d'autant de réseaux monophasés que nécessaire.
Outre le problème d'équilibrage des phases, les tensions de la ligne de T2-T4 sont différentes de celles de celles de la ligne de T2-T3, à cause de la longueur des conducteurs.
Un seul transformateur suffit-il ou en faut-il deux ? En attendant les explications des chapitres suivants, les calculs sont réalisés pour des transformateurs
différents.
Certaines informations manquent et donnent lieu aux hypothèses suivantes.
???p Un réseau triphasé peut être décomposé en trois réseaux monophasés ?
???p La puissance de 36 MW d'un générateur triphasé = 3 x 12 MW/phase ?
???p La tension de ligne à ht est la tension entre phase et neutre. Il semble que la convention soit plutôt la tension entre phases.
Les hypothèses seront vérifiées dans les chapitres ultérieurs.
Les questions suivantes y obtiendront aussi des réponses :
- comment un transfo. triphasé peut-il donner une phase en 254 V pour 10 MW et une autre en 284 V et pour 17 MW ?
Les définitions et règles de base, chapitre 1 Bases, doivent être complétées et nuancées en sachant que l'électricité est un mariage très intime et très complexe
de forces et de courants.
La force longitudinale
La force et le courant longitudinaux, dans l'axe du conducteur, ont été découverts en premier, pour des raisons techniques, courant continu, et historiques, application
de l'effet calorifique de l'électricité, probablement le seul connu au départ.
Les règles originelles datent de cette époque et sont applicables parfaitement dans ce contexte.
La force transversale du champ magnétique
Le développement du courant alternatif, des applications de l'électromagnétisme, alternateurs, moteurs, postes à souder, éclairage fluorescent, et des équipements de
transport, transformateurs, ont fait découvrir l'existence d'autres forces et d'autres courants dans de nombreuses directions.
Principalement, l'utilisation du champ magnétique, amplifié par le passage du courant dans une bobine, a révélé l'existence et l'influence de la fem transversale.
Les règles générales de l'électricité résultent de ces deux forces perpendiculaires et des courants qu'elles induisent.
Observation
La fem s'exerce de façon, à la fois, longitudinale et transversale.
Les lois originelles sont applicables lorsque l'action transversale est négligeable.
Dans le cas contraire, la force résultante détermine les lois généralisées.
Vu sous cet angle, les lois originelles ne sont que des cas particuliers.
Noter qu'il existe toujours une force transversale, même si elle est souvent négligeable, faute d'amplification.
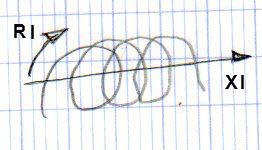
La fem du courant, RI, s'exerce longitudinalement.
Le champ magnétique, amplifié par le bobinage, XI
attire les électrons
perpendiculairement au conducteur
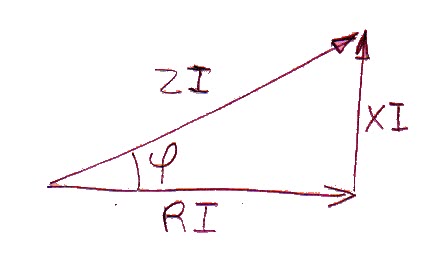
ZI est la résultante de RI et de XI
Explication
(loi d'Ohm généralisée)
Les électrons sont soumis à deux forces, perpendiculaires, proportionnelles à l'intensité. La force longitudinale vaut R x I (V). La transversale vaut X x I (V).
La représentation vectorielle de ces deux forces fait apparaître la force résultante ZI = Z x I (V) et l'angle φ (rad).
Il apparaît clairement que la fem, ou tension, n'est plus RI mais la résultante ZI. En découle la loi d'Ohm généralisée U (V) = Z (Ω) x I (A).
Il apparaît, à la lecture de la littérature scientifique, une imprécision des appellations qui nuit à la compréhension.
Le mot tension, U, désigne à la fois RI et ZI. Pour éliminer les doutes, les tensions seront désormais qualifiées d'active (RI), réactive (XI) et apparente (ZI).
Cette technique, de pure invention, offre l'avantage d'employer les adjectifs utilisés, officiellement et avec la même signification, pour les puissances et les énergies.
Une autre imprécision nuisible concerne l'intensité, le courant.
Les électrons attirés par la force apparente se déplacent dans le sens de cette force et pas dans celui de la force active, ni celui de la force réactive.
Pour éliminer les doutes, les intensités, courants, seront désormais qualifiées d'active (suivant RI), réactive (suivant XI) et apparente (suivant ZI).
Cette technique est, elle aussi, de pure invention

Multiplier chaque côté par n ne change pas φ
Multiplier chaque côté par n ne change pas φ.
Multiplier des forces par 1 / I donne des résistances.
Multiplier des forces par I donne des puissances.
Multiplier des puissances par Δt donnent des travaux ou des énergies.
Cette propriété des triangles rectangles permet d'établir les relations entre φ, les résistances, les forces, les puissances et les énergies.
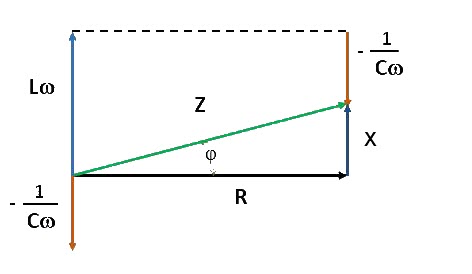
Z2 = R2 + X2
R = Z x cos(φ), X = Z x sin(φ)
(réactance, inductance, henry, vitesse angulaire, impédance, capacitance)
La résistance active s'appelle réellement résistance (R (Ω)). Elle dépend du conducteur, de sa longueur et de sa section. Elle peut être calculée grâce à la formule,
déjà expliquée, ρ x l / S.
La résistance réactive s'appelle réellement réactance (X (Ω)). Elle dépend de la bobine (L (H, henry)) et de la fréquence (f (Hz)). Elle peut être calculée grâce à
la formule 2 x π x f x L ou ω x L.
L représente l'influence de la bobine, inductance, et est exprimée en henry (H).
ω = 2 x π x f exprime la vitesse angulaire de rotation du générateur.
La résistance apparente s'appelle réellement impédance (Z (Ω)). Elle est calculée, depuis Pythagore, grâce à la formule Z2 = R2 + X2.
Une fois l'impédance déterminée, l'intensité apparente, ou la tension apparente, est déterminée par la loi d'Ohm généralisée U = Z x I.
Noter que l'inductance de la bobine (ω.L) peut être corrigée par la capacitance (C (F, farad)) d'un condensateur (1 / ω.C). La réactance X = ω.
L - 1 / ω.C. Positive la réactance est qualifiée d'inductive. Négative elle est appelée réactance capacitive.
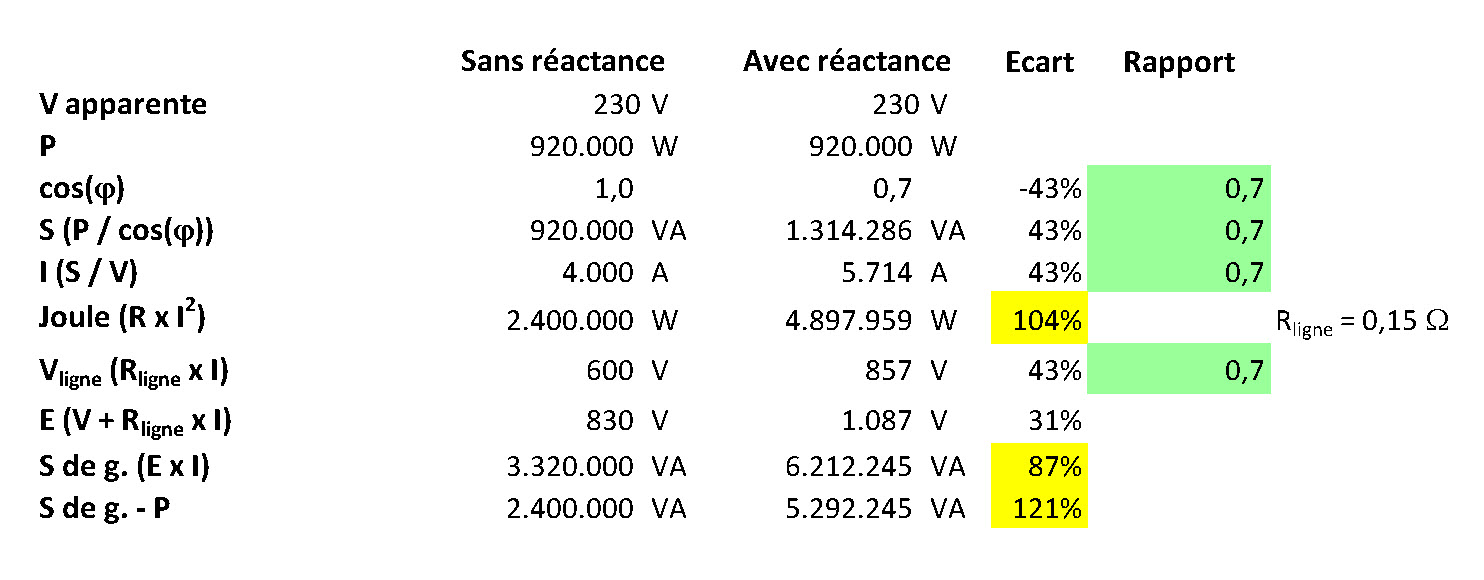
Quartier d'habitation nécessitant une puissance active de 920 kW
Les écarts sont exprimés en pourcents du plus petit nombre
Les rapports sont exprimés en dixièmes du plus grand nombre
Le facteur de puissance, cos(φ), de 0,7 indique que la puissance active vaut 0,7 fois la puissance apparente. Ce rapport se retrouve, bien sûr, entre les puissances
apparentes mais aussi entre les intensités et les pertes de tension occasionnées par la ligne.
Suite à l'augmentation d'intensité, les pertes par effet de Joule s'envolent.
L'augmentation de fem du générateur combinée à l'augmentation d'intensité propulse la puissance apparente du générateur vers les sommets.
Ces calculs démontrent que la production et le transport de puissance réactive occasionnent un très gros problème de puissance.
Il faut augmenter la puissance du générateur, augmenter les investissements, augmenter les consommations d'énergie primaire.
Il faut augmenter la puissance de la ligne, augmenter les investissements.
Tout cela pour subir une augmentation de perte globale de puissance.
Noter que la perte supplémentaire de tension en ligne permet de mesurer la tension réactive présente.
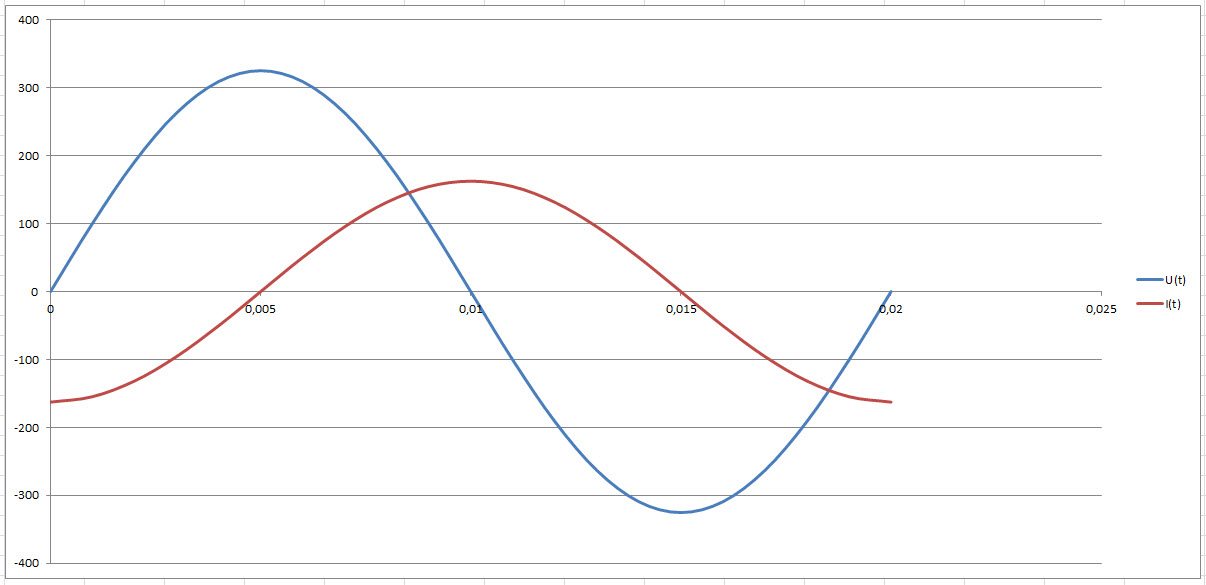
L'auto-induction retarde l'apparition du courant
I = Imax.sin(ωt - φ)
(auto-induction, déphasage)
Le passage de courant dans une bobine provoque un champ magnétique qui crée la puissance réactive nécessaire, par exemple au moteur, mais perturbe le passage du
courant qui prend du retard par rapport à la tension. L'angle de déphasage égale φ, le même que celui évoqué précédemment.
Ici, le courant est perturbé par son propre champ magnétique. Cet effet s'appelle, pour cette raison, auto-induction.
Le courant peut aussi induire une force électromorice apparente qui, au lieu de le ralentir, l'accélère. Les lignes à haute tension ont
cette particularité et le courant y prend de l'avance sur la tension.
La tension est aussi perturbée par la puissance réactive qui la déphase par rapport à elle-même. Ce déphasage apparaît entre le début et la fin
de ligne. L'angle de déphasage est noté δ et appelé angle de transport. La perte de puissance occasionnée est proportionnelle à sin(δ).
Le décalage temporel, déphasage, indique la présence de puissance réactive qui se propage dans le réseau et affecte son fonctionnement, comme
déjà expliqué.
Ces déphasages sont facilement observables et permettent de mesurer la présence de la puissance réactive. Le retard indique une réactance inductive et l'avance une
réactance capacitive.
???s En parallèle, le courant entre dans la branche du moteur sans déphasage. Ressort-il déphasé ? Le déphasage se propage-t-il ? Comment ? Va-t-il chez le voisin ?
Jusqu'où se propage-t-il ainsi ?

Schéma d'un transformateur
Transformateur idéal
Un transformateur idéal est un transformateur virtuel sans aucune perte.
Le rapport de transformation m = U2 / U1 = N2 / N1 où Ni est le nombre de spires du circuit i.
Sans perte, les puissances apparentes sont égales. S1 = U1 x I1 = S2 = U2 x I2.
L'impédance Z2 perçue depuis la source : Z1 = Z2 x (U1 / U2)2.
Transformateur réel
Un transformateur réel présente deux pertes. La perte d'induction au travers de l'armature ferromagnétique, la perte de fer, et la perte par effet de Joule dans les
bobinages, la perte de cuivre.
La perte de fer est constante et indépendante de la charge. Elle est mesurable par un essai à vide. Sans charge au secondaire, le courant primaire est très
faible, l'effet de Joule est très faible et la puissance au primaire est égale à la perte de fer.
Un transformateur n'est pas un récepteur et l'impédance du circuit primaire, en absence de charge secondaire, est quasi infinie.
La perte de cuivre est mesurable en mettant en court-circuit le secondaire. Dans ce cas l'effet de fer est négigeable et la puissance au primaire est égale à
la perte de cuivre.
Ces phénomènes parasites diminuent le rendement du transformateur et différencient le rapport de tension du rapport du nombre de tours.
Une source mentionne 1 % comme estimation possible des pertes d'un transformateur de grande puissance.
Les générateurs doivent ramer dans le même sens
Tous les générateurs connectés au réseau doivent être synchronisés afin de "ramer dans le même sens" et d'éviter que l'un repousse les électrons alors que l'autre
les attire.
Les procédures et techniques de démarrage d'alternateur et de connexion au réseau existent.
L'électricité est très peu stockable. Les efforts consentis pour fabriquer du potentiel doivent donc être, idéalement, équilibrés par de la consommation, donc
du courant.
Idéalement, la production = la consommation car le surplus de production, sauf réserve par batteries et barrages, est perdu.
La fréquence est un indicateur d'équilibre. Si la fréquence diminue, il faut accélérer la production parce que la consommation augmente. Si la fréquence augmente, il faut
ralentir la production parce que la consommation diminue.
L'augmentation de fréquence entraîne une accélération des machines de production, un risque d'endommagement et un arrêt préventif.
La diminution de fréquence entraîne un ralentissement des machines de production, une réduction de production, une incapicité accrue de servir et des risques de délestages
préventifs.
Le triphasé équilibré est le moyen de transport d'électricité le plus répandu pour les raisons déjà invoquées. Mais comment l'équilibre indispensable entre phases,
conditions du transport par trois conducteurs, au lieu de six, est-il préservé ?
La dispersion de plus en plus rapide des productions, grâce aux éoliennes, IPV, cogénérations et autres, confère à cette question une importance croissante.
???p La réponse n'est pas évidente à trouver et les recherches d'information continuent.
L'électricité est devenue indispensable, en un peu plus d'un siècle. La permanence de sa fourniture est essentielle, à la fois pour les utilisateurs privés et
pour les professionnels.
Pour assurer cette permanence, les responsables du tranport et ceux de la distribution doivent veiller à la stabilité des réseaux.
Les principales grandeurs à surveiller sont la fréquence, la tension, l'intensité dans les ouvrages, et la puissance de court-circuit.
La puissance de court-circuit est une valeur conventionnelle égale au produit de la tension nominale et du courant de court-circuit (courant
résultant de la mise à la terre franche des 3 phases).
Les puissances de court-circuit calculées ne peuvent dépasser en aucun nœud du réseau les valeurs limites définies dans le règlement technique. S'il y a dépassement il faut
mettre en oeuvre les moyens de diminuer les puissances de court-circuit en ce nœud ou remplacer les équipements qui introduisent des limitations.
En d'autres termes, les équipements ne doivent pas être détruits par un court-circuit.
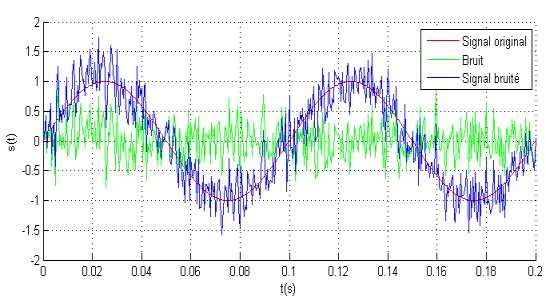
La tension de la ligne rouge est préférable à celle de la bleue
Tous les appareils électriques ne sont pas des ampoules à incandescence. Tous ne se contentent pas d'un frottement d'électrons pour chauffer ou éclairer.
Les moteurs, par exemple, et beaucoup d'autres appareils actuels, sont conçus pour une tension "normale". Il faut que ça monte et descende régulièrement
et sans à-coups.
- La tension doit être voisine de 230 V.
- La fréquence doit être voisine de 50 Hz.
- Les générateurs doivent être synchronisés.
- La courbe représentative de la tension doit être sinusoïdale et exempte de protubérances, bruit.
Le 21ème siècle est celui de la production décentralisée d'électricité.
La raréfaction des sources primaires d'énergie, pétrole, uranium, gaz, charbon, et leur disparition à court terme, ainsi que les progrès techniques ont favorisé, encouragé,
de nouvelles sources permanentes, vent, soleil, marée, autres. Leur éventail très large de puissances et de coûts d'investissement a provoqué une dispersion de la production.
Au lieu de partir d'une seule centrale, l'électricité provient, de plus en plus, d'une multitude de sites connectés à tous les niveaux de tension des réseaux.
La haute et moyenne tension, triphasée et équilibrée, impose des contraintes drastiques de raccordement qui, cela semble logique, permettent le contrôle du réseau.
Le photovoltaïque connecté, en monophasé, au réseau de distribution BT, par contre, constitue un sujet qui attise la curiosité et donne envie de trouver
des réponses.
L'acheminement, par des réseaux "intelligents", de l'électricité produite de façon dispersée vers les consommateurs constitue un autre sujet intriguant.
Description
L'installation photovoltaïque domestique est celle de n'importe quel "Monsieur Dubois". Environ 2010, cinq kWc, bénéficiant du "compteur qui tourne à l'envers" et installée
suite aux promesses fallacieuses de André Antoine
(https://www.youtube.com/watch?v=dVTLfYjuvb4), relayées par Jean-Marc Nollet
(https://www.youtube.com/watch?v=MyoVBWYE-Lo)
,ministres parjures wallons.
Si elle est connectée au réseau de distribution, l'installation transmet son surplus de production et doit être équipée de tout le nécessaire pour assurer la
conformité de tension, de fréquence, de synchronisation et de sécurité. Cette conformité est attestée par un organisme de contrôle après due vérification et
validée par le gestionnaire du réseau de distribution qui procède au raccordement.
Impacts et problèmes potentiels des IPV
Le projet Esprit
Le projet français Esprit a étudié spécifiquement la production photovoltaïque dans le but d'améliorer son intégration au réseau à basse tension.
Ses rapports décrivent objectivement la situation.
(
http://www.photovoltaique.info/IMG/pdf/ESPRIT_Raccordement_des_centrales_PV_au_RPD_BT_en_France.pdf et
http://www.photovoltaique.info/IMG/pdf/esprit_impact_de_l_installation_pv_habitarelle_sur_le_rpd_juillet_2011.pdf
).
Convaincu qu'elle peut être appliquée à la Wallonie, voici les éléments principaux de cette étude.
Les membres du projet Esprit ont inventorié les impacts et problèmes potentiels des IPV évoqués par les experts du monde entier au cours des dernières années.
Les sujets abordés ci-dessous concernent les IPV d'une puissance de production ≤ 5 kWc. Ils représentent 94 % des installations photovoltaïques (99,95 % des
raccordements sont réalisés sur la partie à basse-tension du réseau de distribution, 94 % des installations ont une puissance de production ≤ 5 kWc)
Noter que la puissance de la quasi totalité des IPV correspond à de quoi couvrir les besoins personnels du producteur.
Elévation locale de la tension
Conséquences : découplage d'IPV.
Cette élévation est présentée par plusieurs sources comme l'impact principal des IPV.
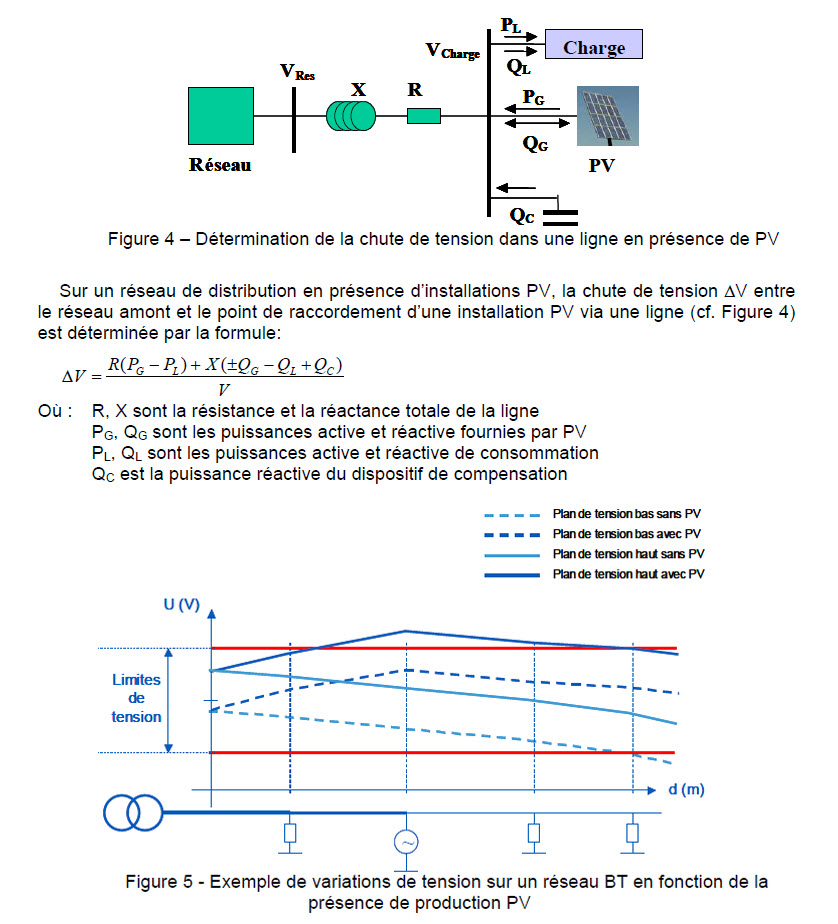
Une installation PV peut provoquer une hausse de tension
Voici l'avis d'un expert contacté grâce au forum forum-photovoltaique.fr
(
http://forum-photovoltaique.fr/viewtopic.php?f=16&t=35279).
"C'est le coeur du fonctionnement d'un onduleur connecté au réseau que de s'adapter aux paramètres locaux pour injecter la puissance à chaque instant. La tension en
sortie de l'onduleur est telle que la puissance DC des panneaux, déduction faite des pertes de conversion, est exactement transmise sur la ligne".
C'est expert est catégorique et déclare que tous les onduleurs élèvent la tension. Malheureusement, tous les spécialistes ne sont pas du même avis. Voici l'avis
d'un autre expert du centre de ressources national sur le photovoltaïque, contacté via le site.
http://www.hespul.org/).
"Sur la façon de produire, d'élever où non sa tension, cela dépend de la technologie".
Ce second expert est plus nuancé. Seuls certains onduleurs élèvent la tension (Synthèse sur les onduleurs).
Il est probable que cette seconde affirmation est la bonne.
De toute façon, les remarques qui suivent sont valables et le resteront aussi longtemps que certains onduleurs élèvent la tension.
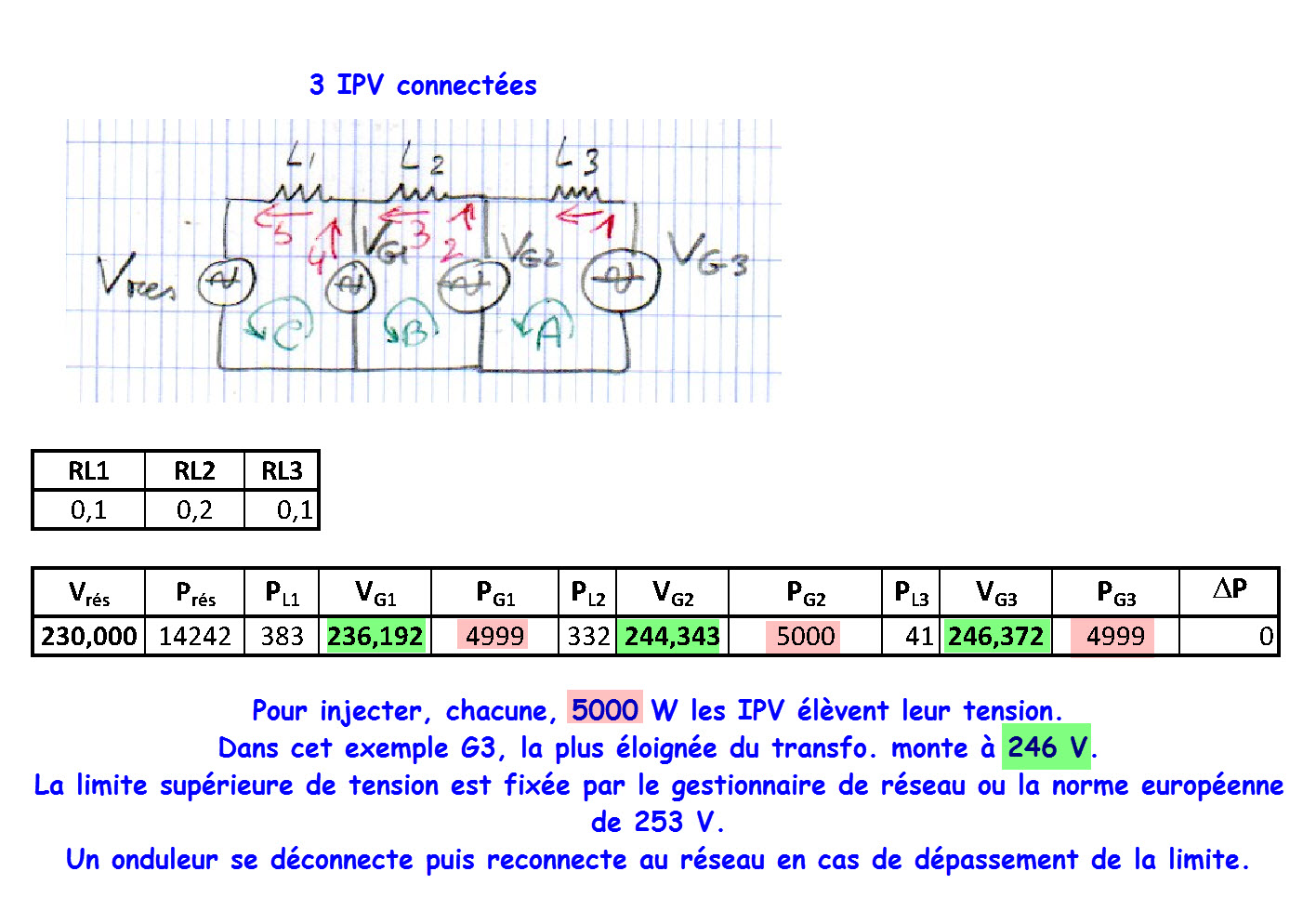
Plus il est loin du départ et plus l'onduleur doit élever la tension
Cette augmentation de tension, en fonction de la puissance à injecter, entraîne certaines installations au-delà de la limite maximale et leur découplage du réseau.
La perte de production occasionnée à certaines peut dépasser les 50 %.
La seconde conséquence de l'injection forcée de puissance PV est le risque d'endommagement des lignes par effet de Joule.
Les chiffres de l'exemple indiquent une puissance de réseau quasiment égale à la somme des puissances injectées par les IPV. Ce cumul, même s'il est impressionnant, ne peut
endommager le réseau dans la mesure où la puissance des IPV est inférieure à la puissance contractuelle de consommation. Si les lignes électriques ne supportent pas la puissance
photovoltaïque, elles supportent encore moins la puissance contractuelle de consommation. Si c'est le cas, c'est le réseau, et lui seul, qui cause un problème.
À CHAUD
Tension
Le GRD impose la tension maximale autorisée. Il ne peut donc y avoir de surtension aux points d'injection. Si certaines IPV doivent se déconnecter, la perte de production
potentielle affecte uniquement les producteurs concernés.
Il ne peut y avoir de problème de surtension que si la tension des IPV dépasse la tension maximale autorisée. Si c'est le cas, la faute incombe à l'organisme certificateur
et au GRD qui ont validé les installations.
Puissance
Il ne peut y avoir de problème de surpuissance que si la puissance cumulée des IPV dépasse la puissance contractuelle de consommation. Dans ce cas,par une belle journée très
ensoleillée, au moment où tous les consommateurs sont absents, le réseau peut surchauffer.
Si c'est le cas, la faute incombe à l'organisme certificateur et au GRD qui ont validé les installations.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -1 / NORMES 0 / IPV 0
Variations rapides de puissance
Conséquences : incertaines.
Causes incertaines.
Le photovoltaïque est structurellement dépendant de l'ensoleillement et de ses variations mais la rapidité de variation de puissance n'est pas mesurée avec précision.
Certaines études indiquent même une lenteur.
À CHAUD
La question reste ouverte.
De toute façon, la réaction à la variation rapide de puissance est une technique maîtrisée de longue date part les électriciens.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
NUL.
GRD -1 / NORMES 0 / IPV 0
Harmoniques de courant
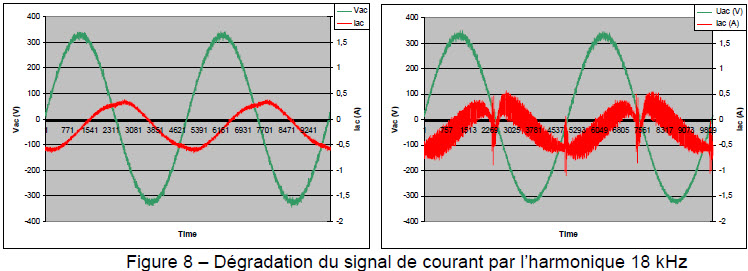
Les aspérités des sinusoïdes sont causées par des ondes parasites appelées harmoniques
Le schéma de droite montre un courant perturbé par un excès de ces harmoniques
À CHAUD
Il semble que la responsabilité de l'IPV est marginale en termes d'harmoniques. Même si c'est très délicat, il faut résoudre le problème là où il se
situe -électronique domestique, éclairage basse consommation, éclairage publique-.
Sachant que les IPV les plus contestables sont le résultat de lacunes règlementaires, des précisions des normes s'imposent.
C'est l'occasion de préciser, par la même occasion, les limites imposées aux IPV fonctionnant à puissance réduite.
Cette fois encore, l'IPV semble peu criticable et les priorités semblent être dans des domaines beaucoup plus sensibles, commercialement et politiquement.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -1 / NORMES -1 / IPV 0
À CHAUD
Il semble d'ores et déjà que la responsabilité de l'IPV est marginale en termes de courant continu.
Des précisions des normes permettront de résoudre le problème.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -1 / NORMES -2 / IPV 0
Contribution aux courants de court circuit
Conséquence : mauvaise coordination du déclenchement des dispositifs de protection du réseau (fusibles et sectionneurs).
Cette influence est négligeable par construction (choix des IGBT -disjoncteurs transistorisés-). Toutefois, ces
conclusions pourraient être à revoir si les onduleurs étaient équipés à l’avenir de fonctions
additionnelles telles que le support à la tension du réseau.
À CHAUD
Pour mémoire.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
Résultat nul.
GRD -1 / NORMES -2 / IPV 0
Impact du PV sur les investissements de réseau
Conséquence : réduction des investissements dans le réseau.
Globalement, la pointe de consommation nationale en période estivale est observée entre 12 h et 16 h, quand la production photovoltaïque est potentiellement présente.
En revanche, la pointe en hiver se situe entre 19h00 et 19h30, quant le photovoltaïque ne produit plus.
La pointe en hiver étant supérieure à la pointe en été, c’est elle qui sera dimensionnante. Ce
niveau d’analyse montre donc que le photovoltaïque ne permet pas de réduire les investissements de réseau au niveau global.
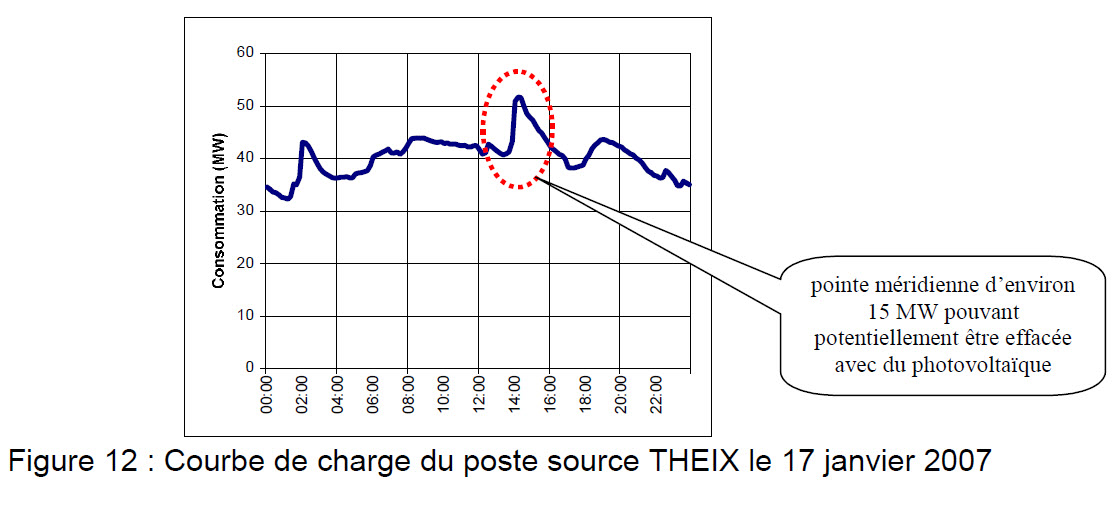
Le PV local permet d'éviter certains transports
À CHAUD
La réduction des coûts n'est pas vérifiable. Il faut noter, encore une fois, qu'aucune augmentation n'est envisagée.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
Résultat nul.
GRD -1 / NORMES -2 / IPV 0
Impact du PV sur les pertes dans les réseaux de distribution
Conséquence : réduction des pertes de transport dans le réseau.
L’énergie produite par le PV résidentiel, étant consommée quasiment sur place, contribue à réduire le transit d’énergie dans les réseaux BT et donc à diminuer
les pertes.
À CHAUD
Avantage indiscuté de l'IPV.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -1 / NORMES -2 / IPV 1
Déséquilibre entre phases
Conséquence : déséquilibre du courant triphasé du réseau.
Le courant triphasé est fourni aux consommateurs ayant besoin d'un peu plus de puissance grâce à une tension de 400 V au lieu de 230 V. En effet, la tension entre
deux phases s'élève à 400 V et plus de tension implique plus de puissance.
Il est fréquent que des installations photovoltaïques raccordées au réseau triphasé soient constituées de trois raccordements monophasés. Si la puissance de
production n’est pas correctement répartie entre les 3 phases d’un même système PV triphasé, alors ce système contribue
à déséquilibrer le réseau BT triphasé.
À CHAUD
Le GRD devrait dire son mot et les normes exiger des raccordements triphasés.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -2 / NORMES -3 / IPV 1
Interaction entre onduleurs
Conséquences : découplages intempestifs ou, au contraire, indétection d'une situation d’îlotage.
Il y a îlotage lorsqu'une partie du réseau est déconnectée du reste et que les producteurs de l'îlot assurent sa charge pendant plus de cinq secondes. Dans ce cas, les IPV de l'îlot doivent se découpler pour garantir la sécurité des intervenants.
De nombreux onduleurs d'un certain type peuvent se perturber les uns les autres.
Ces appareils détectent les situation d'îlotage en envoyant un pic de tension au réseau et en observant la réaction.
S'ils sont synchronisés, c'est-à-dire s’ils injectent la perturbation au même instant, la variation de tension sera plus importante que prévue et la réaction mesurée
pourra par conséquent dépasser le seuil fixé et donc être interprétée à tort comme une situation d’îlotage. A l’inverse, si les onduleurs ne sont pas synchronisés,
les perturbations peuvent s’annuler les unes avec les autres et provoquer une indétection.
Les auteurs soulignent que l'harmonisation des normes pourrait être une solution.
À CHAUD
Les normes, encore les normes.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -2 / NORMES -4 / IPV 1
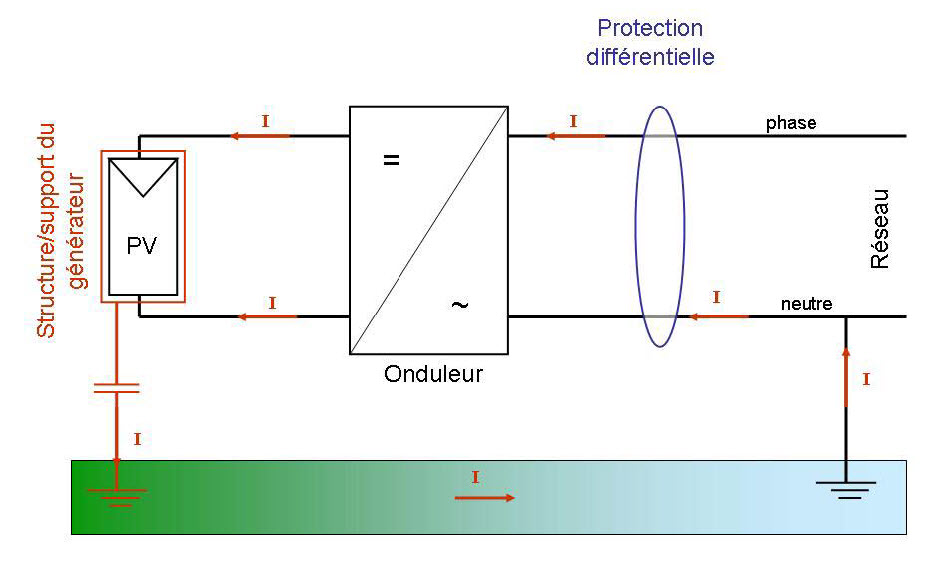
L'installation fait office de condensateur qui envoie du courant à la terre.
Ce courant est transmis par la terre au réseau qui l'interprète comme une fuite et disjoncte.
À CHAUD
Il s'agit apparemment d'une situation très théorique et très improbable. Il faudrait pour en juger disposer de nombres précis.
Ce point est mis en attente.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
Résultat nul.
GRD -2 / NORMES -4 / IPV 1
À CHAUD
L'établissement des bonnes normes résoud le problème.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -2 / NORMES -5 / IPV 1
À CHAUD
Un contrôle lors de la validation et l'établissement des bonnes normes résolvent le problème.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -3 / NORMES -6 / IPV 1
À CHAUD
L'établissement des bonnes normes résoud le problème.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -3 / NORMES -7 / IPV 1
À CHAUD
Les inter-harmoniques ne sont pas imputables aux IPV mais en perturbent le fonctionnement.
C'est au GRD de résoudre ce problème avec les responsables.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -4 / NORMES -7 / IPV 1
À CHAUD
L'établissement des bonnes normes résoud le problème.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
GRD -4 / NORMES -8 / IPV 1
RÉSULTAT DE LA RENCONTRE
Les rapports du projet ESPRIT démontrent que, par ignorance ou par volonté, les politiciens wallons noircissent le tableau.
Nous sommes au début de l'aventure du photovoltaïque. Nous vivons une époque de tâtonnement où les techniques et les normes évoluent simultanément. Il faut faire preuve
de lucidité et de patience.
Malgré tout, le -8 des normes trace la voie. Il faut harmoniser pour développer la communauté. Espérons que nos édiles prendront leurs responsabilités.
D'autant plus que leur influence n'est peut-être pas sans rapport avec le -4 du GRD.
En attendant, avec +1, nous sommes très loin de l'image de l'infâme "prosumer" qui se goinfre sur le dos de la collectivité en laissant le réseau
fondre à cause de la chaleur de son électricité.
Le mot "prosumer" est un horrible wallonicisme destiné par sa laideur à inspirer le dégoût. Il faut le bannir de son vocabulaire.
RÉSULTAT FINAL DE L'ENQUÊTE :
GRD -4 / NORMES -8 / IPV 1
Autres cas où les IPV peuvent apporter leur aide au réseau.
Surfréquence
Les IPV pourraient limiter les hausses de fréquence en réduisant automatiquement la puissance active injectée dans le réseau.
Ecrêtage des pointes de consommation
Il est possible d’écrêter une pointe de consommation en associant aux IPV une capacité de stockage d'énergie chargée en
période de production et déchargée au besoin. Ce service peut être rétribué par les gestionnaires de réseaux.
Une directive européenne sur les énergies renouvelables, adoptée le 23 avril 2009, fixe comme objectif contraignant qu'une part de 20 % de la consommation énergétique au sein
de l'Union provienne de sources d'énergie renouvelables d'ici à 2020.
Pour encourager ses citoyens à investir dans ce domaine, la Région Wallonne propose une série d'avantages pécuniaires, réduction d'impôt, compteur tournant à l'envers,
certificats verts.
En même temps, elle contraint les fournisseurs d'électricité à vendre 12 % d'énergie produite de façon renouvelable et de le prouver en présentant des
certificats verts.
A première vue, il s'agit d'une excellente idée. Les certificats verts achetés aux producteurs PV sont revendus aux fournisseurs à un prix proche de celui de l'électricité
produite avec des énergies irrenouvelables. Les seuls perdants sont les producteurs utilisant ces énergies.
Mais s'agit-il toujours d'une bonne idée en tenant compte du compteur qui tourne à l'envers ?
Démonstration.
La quasi totalité des IPV servent pour satisfaire les besoins personnels des investisseurs. Pour simplifier, imaginons que toute la production PV soit dans ce cas.
Prenons des chiffres simples pour faciliter les calculs. Un ménage sur dix utilise de l'électricité PV et chaque ménage consomme 5000 kWh par an.
Pour 10 ménages, nous obtenons les nombres suivants.
Le ménage PV ne paie pas d'électricité, n'injecte rien dans le réseau et touche 5 CV.
Les 9 autres consomment 45.000 kWh d'électricité pas photovoltaïque pour laquelle les fournisseurs doivent acheter 45 x 0,12 = 5,4 CV, en plus de l'électricité.
Prix de revient = (45 MWh x 65 € / MWh) + (5,4 CV x 65 € / CV) = 3.276 € (au lieu de 2.925 €, soit 12 % de plus).
Prix de vente pas majoré = 45 MWh x 200 € / MWh = 9000 €. Marge sans majoration = 9.000 € - 3.276 € = 5724 € (175 %, au lieu de 6075 €, 208 %, soit 33 % de moins).
Prix de vente majoré du prix de revient = 9000 € + (5,4 CV x 65 € / CV) = 9351 (+ 4 %).
Prix de revient majoré, taux de marge, 208 %, inclus ((PV - 3276) / 3276 = 2,08) = 10.089 € (+ 12 %).
À CHAUD
Si le fournisseur paie tout, sa marge diminue de 208 % à 175 %.
Si le fournisseur ne paie rien, le prix de vente de l'électricité augmente de 12 %.
Avec un taux de marge à 3 chiffres, le fournisseur n'inspire pas vraiment la pitié, le prix de l'électricité pourrait être contrôlé.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
Pas de gouffre financier en vue pour l'instant.
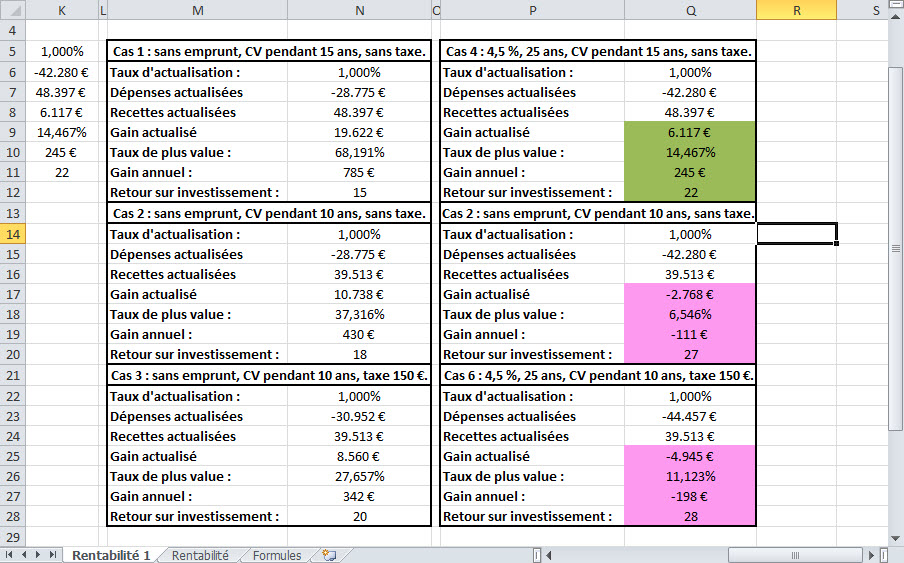
Le gouvernement se trompe de cible.
S'il a acheté en empruntant en 2009, l'investisseur perdra de l'argent.
Quelle est la situation du point de vue de l'investisseur PV ?
Essayons de l'évaluer en conservant a peu près les hypothèses précédentes.
5.700 Wc en 2009 impliquent un investissement de 27.000 € avec un intérêt annuel de 4,5 %. Si la durée de remboursement égale la durée de l'IPV, 25 ans, l'annuité
s'élève à 1.820 €.
5.700 Wc produisent environ 4000 kWh / an.
Prix d'achat de l'électricité pas majoré = 1 MWh x 200 € / MWh = 200 € (au lieu de 5 MWh x 200 € / MWh = 1000 €, soit 800 € de gain).
CV = 7,7 CV / MWh x 4 MWh x 65 € / CV = 2.002 € pendant 15 ans. Pour être très précis, j'ai valorisé le CV à 82 € les 5 premières années.
À CHAUD
Seul l'investisseur qui ne doit pas emprunter a une chance. Dans le cas contraire, les mesures de réductions prévues par le gouvernement vont lui faire boire la
tasse.
RÉSULTAT PROVISOIRE DE L'ENQUÊTE :
L'investisseur PV est loin de la situation dorée dépeinte par les détracteurs. Pire, cette estimation indique que si la durée d'octroi des CV est réduite,
avec ou sans taxe, l'investisseur perdra très probablement de l'argent.
RÉSULTAT DE L'ENQUÊTE :
Par ignorance ou par mensonge, il semble que les politiciens cherchent à berner les citoyens.
Directive européenne de 2009.
Mécanisme des certificats verts.
Le nucléaire est-il toujours l'énergie la plus compétitive ?
Production PV / kWc en Belgique.

IPV ?
Après six mois de recherche documentaire, je crois pouvoir affirmer que la situation est loin d'être aussi claire que l'affirment certains.
Il n'y a pas de problèmes techniques majeurs mais des soucis de démarrage. La mise en place d'un grand nombre d'IPV a montré que les normes devaient être précisées
et parfois corrigées. L'étude montre aussi que les IPV peuvent rendre des services aux GRD, production d'énergie réactive, support en cas de coupure brutale, réduction
des pertes de transport d'électricité.
Financièrement parlant, les investisseurs PV de la première heure ne profitent pas d'une manne mais courent le risque de perdre de lourdes sommes.
J'espère que le bon sens et l'intérêt collectif l'emporteront.
Nombreux sont les sujets passionnants que je n'ai pas eu le temps de creuser.
Le principal est celui des réseaux décentralisés, intelligents ou pas. Comment tranporter l'électricité de centrales photovoltaïques, sahariennes par exemple, pour
approvisionner le nord de l'Europe ? Comment tranporter l'électricité de centrales éoliennes maritimes de la Mer du Nord en Italie ? Le tranport d'énergies injectées
à différentes tensions constitue un enjeu majeur et un investissement colossal.
Plus question des 5.000 Wc du Monsieur Dubois wallon mais je me demande si les "autorités" de Namur ne confondent pas les deux sujets ?
Haut